Unit 7. Correlational Measures

Leyre Castro; J Toby Mordkoff

Unit 7. Correlational Measures

Leyre Castro and J Toby Mordkoff

Summary. In this unit, we will start analyzing how two different variables may relate to one another. We will concentrate on Pearson’s correlation coefficient: how it is calculated, how to interpret it, and different issues to consider when using it to measure the relationship between two variables.

Prerequisite Units

Unit 1. Introduction to Statistics for Psychological Science

Unit 2. Managing Data

Unit 3. Descriptive Statistics for Psychological Research

Unit 6. Brief Introduction to Statistical Significance

Measures of Association

On prior units, we have focused on statistics related to one specific variable: the mean of a variable, the standard deviation of a variable, how the values of a variable are distributed, etc. But often we want to know, not only about one variable, but also how one variable may be related to another variable. So, in this unit we will focus on analyzing the possible association between two variables.

Choice of the appropriate measure of association depends on the types of variables that we are analyzing; that is, it depends on whether the variables of interest are quantitative, ordinal, or categorical, and on the possible range of values of these variables. For example, we may be interested in the differences in healthy lifestyle scores (a continuous quantitative variable) between people who graduated from college and people who did not graduate from college (a categorical variable). Note that this categorical variable has only two values; because of that, it is called a dichotomous variable. In this situation, when one variable consists of numerical, continuous scores, and the other variable has only two values, we use the point-biserial correlation to measure the relationship between the variables.

In other cases, we are interested in how two categorical variables are related. For example, we may want to examine whether ethnic origin is associated to marital status (single, partnership, married, divorced). In this situation, when the two variables are categorical, you use a chi-square as the measure of association.

We could also be interested in the relationship between ordinal variables. If, for example, we want to see if there is a relationship between student rankings in a language test and in a music test, the two variables are ordinal or ranked variables. In this case, when two variables are measured on an ordinal scale, we should use Spearman’s correlation to measure the strength and direction of the association between the variables.

You need to know that these possibilities exist. However, in this unit we are going to focus on the analysis of the relationship between two variables when both variables are quantitative. In this case, we typically use Pearson’s correlation coefficient. For example, when we want to see if there is a relationship between time spent in social media and scores in an anxiety scale. But before looking at this statistical analysis in detail, let’s clarify a few issues.

Correlation as a Statistical Technique

First of all, we need to distinguish between correlational research and correlational statistical analyses. In a correlational research study, we measure two or more variables as they occur naturally to determine if there is a relationship between them. We may read that “as people make more money, they spend less time socializing with others,” or “children with social and emotional difficulties in low-income homes are more likely to be given mobile technology to calm them down,” or “babies’ spatial reasoning predicts later math skills.” The studies supporting these conclusions are correlational because the researcher is measuring the variables “making money,” “time socializing,” “social and emotional difficulties,” and “babies’ spatial reasoning skills,” rather than manipulating them; that is, the researcher is measuring these variables in the real word, rather than determining possible values of these variables and assigning groups to specific values. When we say that a study is correlational in nature we are referring to the study’s design, not the statistics used for analysis. In some situations, the results from a correlational study are analyzed using something other than a correlational statistic. Conversely, the results from some experiments, in which one of the variables was determined by the experimenter, such as the number of dots on a computer screen, can be analyzed using a correlational statistic. Thus, it is important to understand when is appropriate to use a correlational statistical technique.

When we analyze a correlation, we normally are looking at the relationship between two numerical variables, so that we have 2 scores for each participant. If we want to see whether spatial skills at the age of 4 correlate with mathematical skills at the age of 12, then we will have one score for spatial skills at 4, and one score for mathematical skills at 12, for each individual participating in our study.

These scores can be represented graphically in a scatterplot. In a scatterplot, each participant in the study is represented by a point in two-dimensional space. The coordinates of this point are the participant’s scores on variables X (in the horizontal axis) and Y (in the vertical axis).

How we decide which variable goes on the abscissa (x-axis) or on the ordinate (y-axis) depends on how we interpret the underlying relationship between our variables. We may have a predictor variable that is related to an outcome (also called response or criterion variable), as in the case of spatial skills at the age of 4 (predictor) and mathematical skills at the age of 12 (outcome). In this case, the predictor variable is represented on the x-axis, whereas the outcome variable is represented on the y-axis, as shown in Figure 7.1.

This distinction between predictor and outcome variables may be obvious in some cases; for example, smoking will be the predictor and whether or not lung cancer develops will be the outcome, or healthy diet will be the predictor and cardiovascular disease the outcome. But may not always be; for example, time to complete a task may be related to accuracy in that task, but it is not clear whether accuracy depends on time or time depends on accuracy. In this latter case, it does not matter which variable is represented on the x-axis or the y-axis. However, when creating a scatterplot, be aware that most people will have a tendency to interpret the variable in the x-axis as the one leading to the variable in the y-axis.

A scatterplot provides you with a quick visual, intuitive way to assess the correlation between the two variables. It could be that there is no correlation, or the correlation is positive, or negative, as illustrated in Figure 7.1.

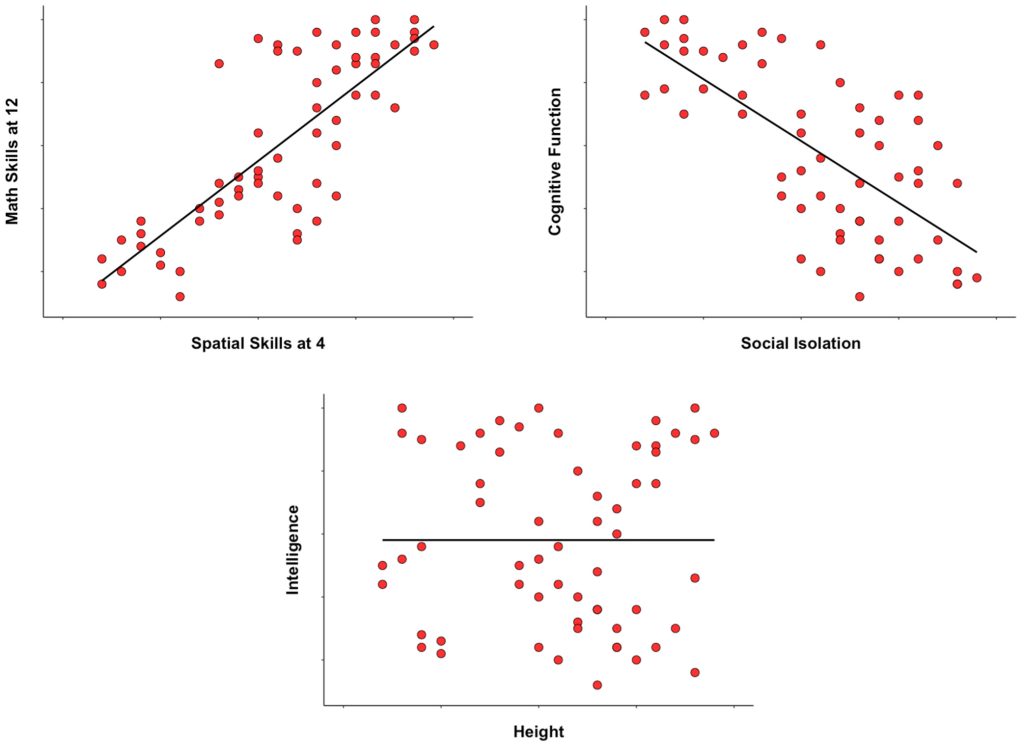
Scatterplots — Figure 7.1. Three scatterplots depicting different types of relationships. On the top left, a scatterplot showing a positive relationship between spatial skills at the age of 4 and mathematical skills at the age of 12. On the top right, a scatterplot showing a negative relationship between social isolation and cognitive functioning in the elderly. On the bottom, a scatterplot showing no relationship between height and intelligence. The straight lines show the trend of the linear relationship between the variables.

If spatial skills in 4-year olds are related to mathematical skills at the age of 12, so that children who at the age of 4 show poor spatial skills tend to show poor mathematical skills eight years later, and children who at the age of 4 show good spatial skills tend to show good mathematical skills eight years later, then there is a positive correlation between spatial skills at the age of 4 and mathematical skills at the age of 12. This positive correlation, where the two variables tend to change in the same direction, is represented on the top left panel. On the top right panel we see an example of a negative correlation. In this case, it was observed that, in the elderly, the higher the social isolation, the lower their cognitive functioning. The correlation is negative because the two variables go in opposite directions: as social isolation increases, cognitive functioning decreases. On the bottom panel, height and intelligence are depicted. In this case, the data points are distributed without showing any trend, so there is no correlation between the variables.

Pearson’s Correlation Coefficient

Visual inspection of a scatterplot can give us a very good idea of how two variable are related. But we need to conduct a statistical analysis to confirm a visual impression or, sometimes, to uncover a relationship that may not be very obvious. There are different correlational analysis, depending on the type of relationship between the variables that we want to analyze. When we have two quantitative variables that change together—so that when one of the variables increases, the other variable increases as well, or when one of the variables increases, the other variable decreases—the most commonly used correlational analysis is Pearson product-moment correlation, typically named Pearson’s correlation coefficient or Pearson’s r or just r.

In order to use Pearson’s correlation coefficient:

Both variables must be quantitative. If the variables are numerical, but measured along an ordinal scale, Spearman coefficient should be used, instead.
The relationship between the two variables should be linear. Pearson’s correlation coefficient can only detect and quantify linear (i.e., “straight-line”) relationships. If the data in the scatterplot show some kind of curvilinear trend, then the relationship is not linear and a more complicated procedure should be used, instead.

Pearson’s correlation coefficient measures the direction and the degree of the linear relationship between two variables. The value of r can range from +1 (perfect positive correlation) to -1 (perfect negative correlation). A value of 0 means that there is no correlation. The sign of r tells you the direction (positive or negative) of the relationship between variables. The magnitude of r tells you the degree of relationship between variables. Let’s say that we obtain a correlation coefficient of 0.83 between physical activity (exercise hours per week) and scores on an academic test. What does it mean? Since 0.83 is positive and close to 1.00, you can say that the two variables have a strong positive relationship –so high number of exercise hours per week are related to high scores on the academic test. In a different situation, let’s say that we obtain a correlation coefficient of -0.86 between number of alcoholic drinks per week and scores on an academic test. What does it mean? Since -0.86 is negative and close to -1.00, you can say that the two variables have a strong negative relationship –so high number of alcoholic drinks per week are related to low scores on the academic test.

A slightly more complicated way to quantify the strength of the linear relationship is by using the square of correlation: R². The reason why this is sometimes preferred is because R² is the proportion of the variability in the outcome variable that can be “explained” by the value of the predictor variable. If we obtain an R²of 0.23 when analyzing the relationship between spatial skills at the age of 4 (predictor) and mathematical skills at the age of 12 (outcome), we will say that spatial skills at the age of 4 explain 23% of the variability in mathematical skills at the age of 12. This amount of explained variance is one way of expressing the degree to which some relation or phenomenon is present.

Importantly, when you use R² as your measure of strength, you can make statements like “verbal working memory score is twice as good at predicting IQ than spatial working memory score” (assuming that the R² for verbal WM and IQ is twice as large as the R² for spatial WM and IQ). You cannot make statements of this sort based on (unsquared) values of r.

Conceptually, Pearson’s correlation coefficient computes the degree to which change in one numerical variable is associated with change in another numerical variable. It can be described in terms of the covariance of the variables, a measure of how two variables vary together. When there is a perfect linear relationship, every change in the X variable is accompanied by a corresponding change in the Y variable. The result is a perfect linear relationship, with X and Y always varying together. In this case, the covariability (of X and Y together) is identical to the variability of X and Y separately, and r will be positive (if the two variables increase together) or negative (if increases in one variable correspond to decreases in the other variable).

To understand the calculations for r, we need to understand the concept of sum of products of deviations (SP). It is very similar to the concept of sum of squared deviations (SS) that we saw in Unit 3 to calculate the variance and standard deviation.

This was the formula for the SS of one single variable, X:

$\ SS_x = \sum {(X_i - \bar {X})^2}$

In order to see the similarities with the SP, it will be even clearer if we write the formula for the SS this way:

$\ SS_x = \sum {(X_i - \bar {X})}{(X_i - \bar {X})}$

The formula for the sum of the products of the deviation scores or SP computes the deviations of each score for X and for Y from its corresponding mean, and then multiplies and add those values:

$\ SP_x_y = \sum {(X_i - \bar {X})}{(Y_i - \bar {Y})}$

In order to show the degree to which X and Y vary together, that is, their covariance (similar to the variance for one variable, but now referring to two variables), we divide by n – 1:

$\begin{equation*} \ cov_x_y = \frac {\sum (X_i - \bar {X})(Y_i - \bar {Y})} {n - 1} \end{equation*}$

Practice (1)

Let’s calculate the SP and the covariance with the dataset containing the number of study hours before an exam (X), and the grade obtained in that exam (Y), for 15 participants, that we used previously in Unit 3. The table shows each of the scores, the deviation scores for each X and Y score, and the product of each pair of deviation scores:

Part.	Hours	Grade	$(X_i - \bar {X})$	$(Y_i - \bar {Y})$	$(X_i - \bar {X}) (Y_i - \bar {Y})$
P1	8	78	(8 – 13.66)	(78 – 86.46)	-5.66 * -8.46 = 47.88
P2	11	80	(11 – 13.66)	(80 – 86.46)	-2.66 * -6.46 = 17.18
P3	16	89	(16 – 13.66)	(89 – 86.46)	2.34 * 2.54 = 5.94
P4	14	85	(14 – 13.66)	(85 – 86.46)	0.34 * -1.46 = – 0.50
P5	12	84	(12 – 13.66)	(84 – 86.46)	-1.66 * -2.46 = 4.08
P6	15	86	(15 – 13.66)	(86 – 86.46)	1.34 * -0.46 = – 0.62
P7	18	95	(18 – 13.66)	(95 – 86.46)	4.34 * 8.54 = 37.06
P8	20	96	(20 – 13.66)	(96 – 86.46)	6.34 * 9.54 = 60.48
P9	10	83	(10 – 13.66)	(83 – 86.46)	-3.66 * -3.46 = 12.66
P10	9	81	(9 – 13.66)	(81 – 86.46)	-4.66 * -5.46 = 25.44
P11	16	93	(16 – 13.66)	(93 – 86.46)	2.34 * 6.54 = 15.30
P12	17	92	(17 – 13.66)	(92 – 86.46)	3.34 * 5.54 = 18.50
P13	13	84	(13 – 13.66)	(84 – 86.46)	-0.66 * -2.46 = 1.62
P14	12	83	(12 – 13.66)	(83 – 86.46)	-1.66 * -3.46 = 5.74
P15	14	88	(14 – 13.66)	(88 – 86.46)	0.34 * 1.54 = 0.52

Now, as the term $\sum {(X_i - \bar {X})}{(Y_i - \bar {Y})}$ in the formula indicates, we need to add all the products of each pair of deviation scores, the scores in the rightmost column. This total adds up to 251.33. Then, we divide by n -1, that is, by 14:

$\begin{equation*} \ cov_x_y = \frac {251.33} {14} = 17.95 \end{equation*}$

Thus, the covariance between Hours and Grade is 17.95.

It could be possible to use the covariance between X and Y as a measure of the relationship between the two variables; however, its value is not quickly understandable or possible to compare across studies because it depends on the measurement scale of the variables, that is, it depends on the specific units of X and the specific units of Y. Pearson’s correlation coefficient solves this issue, by dividing the covariance by the specific value of the standard deviations of X and Y, so that the units (and scale effects) cancel:

$\begin{equation*} \ r = \frac {cov_x_y} {s_x s_y} \end{equation*}$

With this maneuver, the limits of r range between -1 and +1 and, therefore, r is easy to interpret, and its value can be used to compare different studies.

Practice (2)

Let’s calculate Pearson’s correlation coefficient in our case. We know from Unit 3 that the standard deviation of X, the number of hours, is 3.42, and that the standard deviation of Y, the grade, is 5.53. Therefore:

$\begin{equation*} \ r = \frac {17.95} {3.42 * 5.53} = 0.95 \end{equation*}$

So, Pearson’s correlation coefficient between number of hours studying and grade obtained in our dataset is 0.95. Very high.

As indicated above, the magnitude of r tells us how weak or strong the relationship is so, the closer to 0, the weaker the relationship is, whereas the closer to 1 (or -1), the stronger the relationship is. Figure 7.2 shows different scatterplots illustrating different values of r.

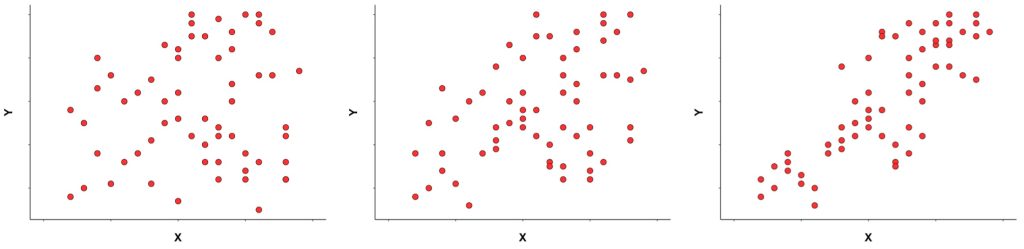
A perfect correlation of +1 or -1 means that all the data points lie exactly on a straight line. These perfect relationships are rare, in general, and very unlikely in psychological research.

Interpretation of Pearson’s Correlation Coefficient

The interpretation of the value of the correlation coefficient r is somehow arbitrary (see Table 7.1 for typical guidelines). Although most data scientists will agree that an r smaller than 0.1 reflects a negligible relationship, and an r larger than 0.9 reflects a very strong relationship, how to interpret intermediate coefficients is more uncertain. An r value of 0.42 may be weak or strong depending on the typical or possible association found between some given variables. For example height and weight are typically highly correlated, so an r value of 0.42 between those variables would be low; however, an r value of 0.42 between eating cranberries daily and cognitive capacity would be high, given that so many other variables are related to cognitive capacity. It also may be weak or strong depending on the results of other research studies in the same area. Thus, a specific r value should be interpreted within the context of the specific research.

Value of r	Strength
0.0 to 0.09	negligible
0.1 to 0.29	weak
0.3 to 0.49	moderate
0.5 to 0.89	strong
0.9 to 1.00	very strong

Table 7.1. Typical guidelines for the interpretation of r

Issues to Consider

Outliers

An outlier is a data point that has a value much larger or smaller than the other values in a data set. It is important to carefully examine the dataset for outliers because they can have an excessive influence on Pearson’s correlation coefficient. For example, in Figure 7.3, we can see a data point that has X and Y values much larger than the other data points. Pearson’s r for this entire data set is r = 0.86, indicating a strong relationship between X and Y. However, if we do not include the outlier in the analysis, Pearson’s r is greatly reduced, r = 0.07, very close to 0, indicating a negligible relationship. You should be able to easily visualize the difference with and without the outlier data point in the scatterplot in Figure 7.3.

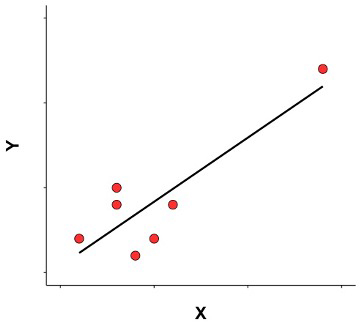
Scatterplot with outlier — Figure 7.3. Scatterplot of the relationship between two variables, X and Y, with one outlier in the data set.

You always need to examine the distribution of your scores to make sure that there are no relevant outliers. Whether outliers should or should not be eliminated from an analysis depends on the nature of the outlier. If it is a mistake in the data collection, it should probably be eliminated; if it is an unusual, but still possible value, it may need to be retained. One way or the other, the presence of the outlier should be noted in your data report. If the outlier must be retained, an alternative analysis can be Spearman correlation, that is more robust than Pearson’s correlation coefficient against outliers.

Restricted Range

You need to be aware that the value of a correlation can be influenced by the range of scores in the dataset used. If a correlation coefficient is calculated from a set of scores that do not represent the full range of possible values, you need to be cautious in interpreting the correlation coefficient. For example, you may be interested in the relationship between family income level and educational achievement. You choose a convenient sample in a nearby school, that happens to be a private school in which most students come from wealthy and very wealthy families. You analyze the data in your sample and find that there is no correlation between family income level and educational achievement. It could be that, indeed, this relationship is not apparent among high-income students, but it would have been revealed if you have included in your sample students from very-low, low, and middle-income families. Figure 7.4 shows a scatterplot that depicts this issue.

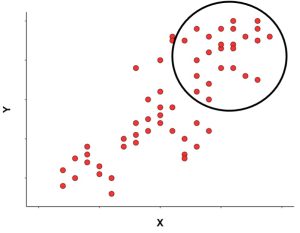
Scatterplot — Figure 7.4. Considering all the possible values for X and Y in this scatterplot, r = 0.80. However, if the data set consisted of a restricted range of values, as those high values included in the circle, r would be close to 0.

In general, in order to establish whether or not a correlation exists between two variables, you need a wide range of values for each of the variables. If it is not possible to obtain this wide range of values, then at least you should limit your interpretation to the specific range of values in your dataset.

Correlation Coefficient in the Sample and in the Population

We rarely are interested in the correlation between variables that only exists in a sample. As is true for most situations, we use the correlation coefficient in our sample to make an estimate of the correlation in the population. How does that work? The sample data allow us to compute r, the correlation coefficient for the sample. We normally do not have access to the entire population, so we cannot know or calculate the correlation coefficient for the population (named rho, ρ). Because of this, we use the sample correlation coefficient, r, as our estimate of the unknown population correlation coefficient . The accuracy of this estimation depends on two things. First, the sample needs to be representative of the population; for example, the people included in the sample need to be an unbiased, random subset of the population—this is not a statistical issue, but it should always be kept in mind. Second, how precisely a sample correlation coefficient will match the population correlation coefficient depends on the size of the sample: the larger the sample, the more accurate the estimate (provided that the sample is representative).

Whenever some value that is calculated from a sample is used to estimate the (true) value in the population, the question of bias arises. Recall that bias is whether the estimator has a tendency to over-shoot or under-shoot the target value. If possible, we always use the estimator that has the least bias.

In the case of correlation coefficients, the value of r from a sample provides a very good estimate of ρ in the population, as long as the sample size is not very small. If you are working with samples of fewer than 30 participants, you may wish to adjust the value of r when using it as an estimate of ρ. The details of this adjustment are beyond the scope of this unit, but you should be aware that better estimates of ρ are available for small-sample situations.

Before conducting our study, we need to decide the size of our sample. This decision must be informed by the purpose of minimizing inaccurate estimates when we later analyze our sample data. So, we need to plan for the sufficient sample size. It is not easy to give a specific number, because our sample size should be based on prior and expected sizes of the relationship of interest. And, the size of the sample should be large enough to be able to detect small effects, and make sure that our results are not due to chance. Nowadays, there are a variety of software tools that can help you decide the size of the sample. At the moment, just be aware that, if you have a sample that is too small, the correlation coefficient that you obtain from your sample data may be inadequate as the correlation coefficient for the population.

In addition, in order to improve the interpretation of your correlation coefficient r, a confidence interval will help. That’s why is always advisable to include a confidence interval for the obtained coefficient (typically, a 95% confidence interval). The confidence interval provides the range of likely values of the coefficient in the population from which the sample was taken. An r value of 0.53 suggests quite a strong relationship between two variables; however, if the 95% confidence interval ranges from 0.02 to 0.82 (as it could be the case with a very small sample), then the strength of the relationship in the population could be negligible (r = 0.02) and, therefore, of little importance, or it could be strong (r = 0.82) and, therefore, of high relevance. So, if the confidence interval is very wide, it is difficult to make a valuable interpretation of the results. In general, a narrower confidence interval will allow us for a more accurate estimation of the correlation in the population.

Conclusions

A correlation coefficient shows the strength and direction of an association between two variables. Note that a correlation describes a relationship between two variables, but does not explain why. Thus, it should never be interpreted as evidence of a causal relationship between the variables.

If r is relatively strong, you can assume that when one variable increases, the other variable will increase as well (for a positive relation) or the other variable will decrease (for a negative relation). But r does not allow you to predict, precisely, the value of one variable based on the value of the other variable. To do that, we have another statistical tool: linear regression analysis (Unit 9)

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Data Analysis in the Psychological Sciences: A Practical, Applied, Multimedia Approach Copyright © 2023 by Leyre Castro & J Toby Mordkoff is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.