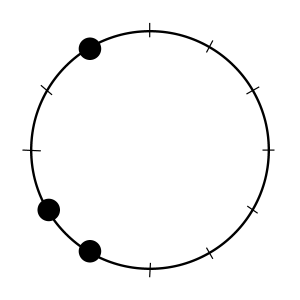
A pitch-class set (or pitch-class collection) is a group of pitch classes. Pitch-class sets can be used as scales, chords, melodies, and combinations of chords and melodies. Equivalent pitch-class sets belong to the same set class. The most commonly referenced set classes are trichords.

History

Pitch-class sets have been used as long as people have used groups of notes without regard to register (without regard to which octave). However, the notion is associated with some twentieth- and twenty-first-century music where other melodic and harmonic concepts are difficult or impossible to apply. After Allen Forte developed the theory in the 1970s for analysis, some musicians such as Elliott Carter have used it for composition.

General properties

Sets are equivalent if they can be mapped onto one another through transposition (shifting up or down) or inversion (turning upside down). These operations translate into rotation and flipping on the clock face. For example, the pitch-class sets G–G#–B, A–Bb–Db, and Db–E–F are equivalent, because G–G#–B can be shifted onto A–Bb–Db, and A–Bb–Db can be flipped onto Db–E–F:

Example: Arnold Schoenberg, No. 1 of Three Piano Pieces, op. 11 (1909): The opening measures feature the pitch-class sets discussed above.

Equivalent pitch-class sets belong to the same set class. The most common label for a set class is like a list of intervals. Technically, it is a list of pitch classes, but this book does not use pitch-class numbers. To determine the set class of a pitch-class set:

1. Find the most packed list of pitch classes, which will exclude the widest gap on the clock face. In the case of G–G#–B, the most packed list is G–G#–B, which excludes the widest gap of 8 semitones (B–G).
2. Read the intervals from the end with the narrower interval. In the case of G–G#–B, G–G# is smaller than B–G#, so the intervals are read from G. The intervals are 0 (G–G), 1 (G–G#), and 4 (G–B), so the set class represented by G–G#–B (and A–Bb–Db, etc.) is (014).

Pitch-class sets can be related in other ways besides equivalence, such as inclusion (where one set is included in another) or intersection (where two sets have a common subset). Set classes can also be related by inclusion and intersection.

Specific sizes

Dyad

A dyad is a pair of pitch classes. There are six dyad set classes:

 

 

These six dyad set classes are similar to the seven interval classes 0–6:

 

 

An interval class includes both the interval it is named for and its inversion. For example, interval class 1 includes intervals 1 and 11 (e.g., m2 and M7, or A1 and d8). In the case of interval 6, the inversion is also 6.

Trichord

A trichord is a group of three pitch classes. All the trichord set classes are distinctive, and a couple have nicknames. (012), the chromatic trichord, is every three-note segment in a chromatic, and it has the same intervals reading up (here from C) and reading down (from Ebb). (013) is every three-note segment in an octatonic scale. (014) is every three-note segment in a hexatonic scale. (015) is like an incomplete major seventh chord:

 

 

(016) is called the Viennese trichord, because it is a favorite of the Second Viennese School. Whether placed right side up or upside down, (016) can be voiced as altered fourth chords. It might seem that you could have an (017), but actually it is (016) again:

 

(024) is every three-note segment in a whole-tone scale, and it has the same intervals reading up (here from C) and reading down (from E). (025) is like an incomplete minor seventh chord. (026) right side up is like an incomplete dominant seventh chord, while (026) upside down is like an incomplete half-diminished seventh chord. (027) is like a fourth chord. Like (012) and (024), but less obviously, (027) has the same intervals reading up (here from C) and reading down (from D):

 

(036) is like a diminished triad. (037) is like a major triad or minor triad. And (048) is like an augmented triad. It is the only trichord that has the same intervals reading up and reading down from any note, because its members are equidistant in pitch-class space (it forms an equilateral triangle on the clock face):

 

Larger sets

Pitch-class sets with four, five, and six members are called tetrachords, pentachords, and hexachords. There are also terms for sets with seven, eight, nine, ten, eleven, and twelve members, but these terms are rarely used. The letters T and E (or t and e) are used for pitch classes 10 and 11 in the names of larger set classes. (Some texts use A and B for pitch classes 10 and 11, i.e., Bb and B, which is terribly confusing.)

Example: Alban Berg, “Schlafend trägt man mich in mein Heimatland,” no. 2 of 4 Gesänge, op. 2 (1910): All the chords in the piano are (0268) tetrachords.

Further reading

• Stephen Kostka, Materials and Techniques of Post-Tonal Music, Chapter 9
• Miguel Roig-Francolí, Understanding Post-Tonal Music, Chapter 3
• Joseph Straus, Introduction to Post-Tonal Theory, Chapter 2

External links

The Wikipedia article on set theory is informative but very dense. It uses numbers for pitch classes.