Electric generators induce an emf by rotating a coil in a magnetic field, as briefly discussed in Chapter 23.1 Induced Emf and Magnetic Flux. We will now explore generators in more detail. Consider the following example.

Example 1: Calculating the Emf Induced in a Generator Coil

The generator coil shown in Figure 1 is rotated through one-fourth of a revolution (from $latex \boldsymbol{\theta = 0^{\circ}} $ to $latex \boldsymbol{\theta = 90^{\circ}} $) in 15.0 ms. The 200-turn circular coil has a 5.00 cm radius and is in a uniform 1.25 T magnetic field. What is the average emf induced?

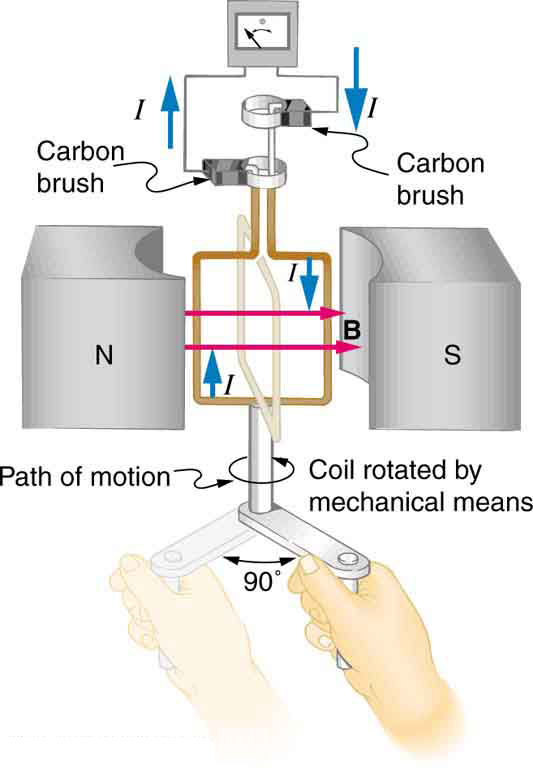
Strategy

We use Faraday’s law of induction to find the average emf induced over a time $latex \boldsymbol{\Delta t} $:

$latex \boldsymbol{\textbf{emf} = -N} $

We know that $latex \boldsymbol{N = 200} $ and $latex \boldsymbol{\Delta t = 15.0 \;\textbf{ms}} $, and so we must determine the change in flux $latex \boldsymbol{\Delta \phi} $ to find emf.

Solution

Since the area of the loop and the magnetic field strength are constant, we see that

$latex \boldsymbol{\Delta \phi = \Delta(BA \;\textbf{cos} \;\theta) = AB \Delta(\textbf{cos} \;\theta)} $

Now, $latex \boldsymbol{\Delta (\textbf{cos} \;\theta) = -1.0} $, since it was given that $latex \boldsymbol{\theta} $ goes from $latex \boldsymbol{0^{\circ}} $ to $latex \boldsymbol{90^{\circ}} $ . Thus $latex \boldsymbol{\Delta \phi = -AB} $, and

$latex \boldsymbol{\textbf{emf} = N} $

The area of the loop is $latex \boldsymbol{A = \pi r^2 = (3.14 \cdots )(0.0500 \;\textbf{m})^2 = 7.85 \times 10^{-3} \;\textbf{m}^2} $. Entering this value gives

$latex \boldsymbol{\textbf{emf} = 200} $ $latex \boldsymbol{= 131 \;\textbf{V}} $.

Discussion

This is a practical average value, similar to the 120 V used in household power.

The emf calculated in Example 1 is the average over one-fourth of a revolution. What is the emf at any given instant? It varies with the angle between the magnetic field and a perpendicular to the coil. We can get an expression for emf as a function of time by considering the motional emf on a rotating rectangular coil of width $latex \boldsymbol{w} $ and height $latex \boldsymbol{ \ell} $ in a uniform magnetic field, as illustrated in Figure 2.

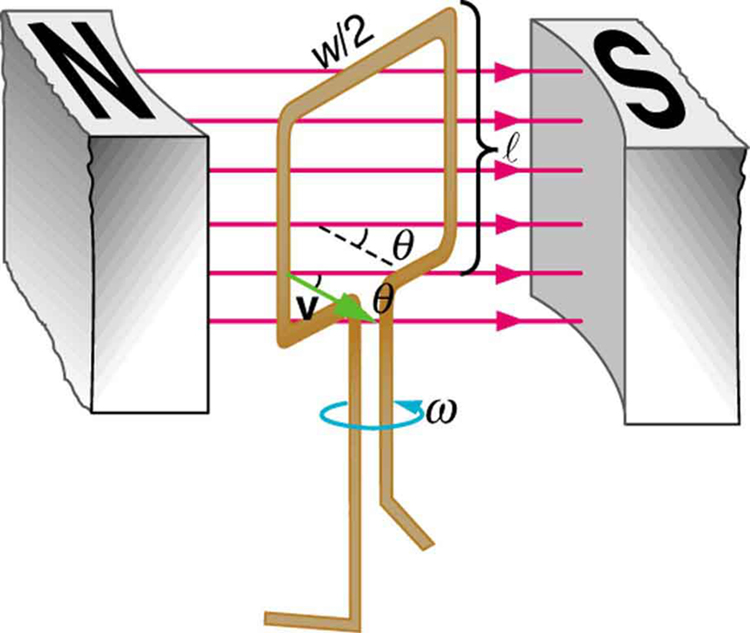
Charges in the wires of the loop experience the magnetic force, because they are moving in a magnetic field. Charges in the vertical wires experience forces parallel to the wire, causing currents. But those in the top and bottom segments feel a force perpendicular to the wire, which does not cause a current. We can thus find the induced emf by considering only the side wires. Motional emf is given to be $latex \boldsymbol{\textbf{emf} = B \ell v} $, where the velocity $latex \boldsymbol{v} $ is perpendicular to the magnetic field $latex \boldsymbol{B} $. Here the velocity is at an angle $latex \boldsymbol{\theta} $ with $latex \boldsymbol{B} $, so that its component perpendicular to $latex \boldsymbol{B} $ is $latex \boldsymbol{v \;\textbf{sin} \;\theta} $ (see Figure 2). Thus in this case the emf induced on each side is $latex \boldsymbol{emf = B \ell v \;\textbf{sin} \theta} $, and they are in the same direction. The total emf around the loop is then

This expression is valid, but it does not give emf as a function of time. To find the time dependence of emf, we assume the coil rotates at a constant angular velocity $latex \boldsymbol{\omega} $. The angle $latex \boldsymbol{\theta} $ is related to angular velocity by $latex \boldsymbol{\theta = \omega t} $, so that

Now, linear velocity $latex \boldsymbol{v} $ is related to angular velocity $latex \boldsymbol{\omega} $ by $latex \boldsymbol{v = r \omega} $. Here $latex \boldsymbol{r = w/2} $, so that $latex \boldsymbol{v = (w/2) \omega} $, and

$latex \boldsymbol{emf = 2B \ell} $ $latex \boldsymbol{\omega \;\textbf{sin} \omega t =(\ell w) B \omega \;\textbf{sin} \omega t}. $

Noting that the area of the loop is $latex \boldsymbol{A = \ell w} $, and allowing for $latex \boldsymbol{N} $ loops, we find that

is the emf induced in a generator coil of $latex \boldsymbol{N} $ turns and area $latex \boldsymbol{A} $ rotating at a constant angular velocity $latex \boldsymbol{\omega} $ in a uniform magnetic field $latex \boldsymbol{B} $. This can also be expressed as

where

is the maximum (peak) emf. Note that the frequency of the oscillation is $latex \boldsymbol{f= \omega /2 \pi} $, and the period is $latex \boldsymbol{T = 1/f=2 \pi / \omega} $. Figure 3 shows a graph of emf as a function of time, and it now seems reasonable that AC voltage is sinusoidal.

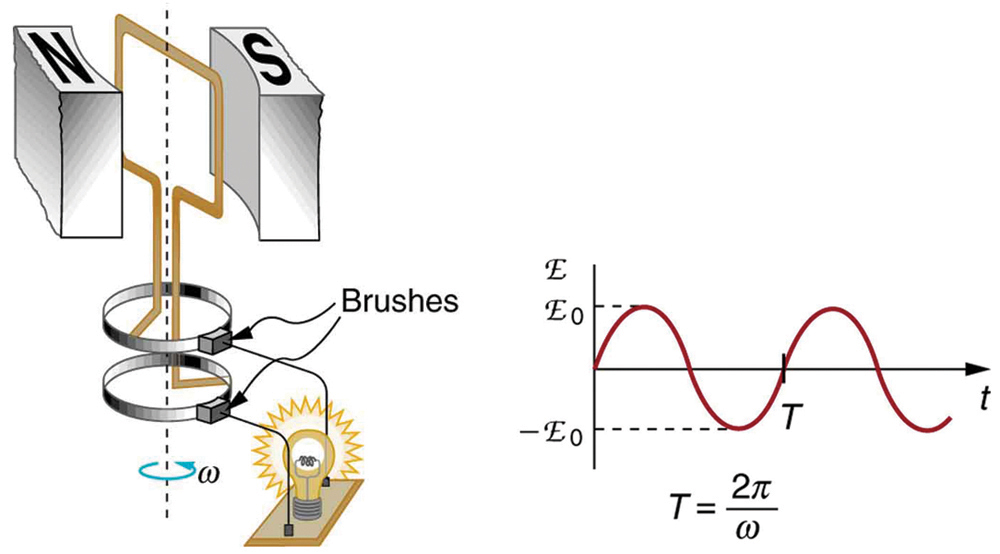
The fact that the peak emf, $latex \boldsymbol{emf_0 = NAB \omega} $, makes good sense. The greater the number of coils, the larger their area, and the stronger the field, the greater the output voltage. It is interesting that the faster the generator is spun (greater $latex \boldsymbol{\omega} $), the greater the emf. This is noticeable on bicycle generators—at least the cheaper varieties. One of the authors as a juvenile found it amusing to ride his bicycle fast enough to burn out his lights, until he had to ride home lightless one dark night.

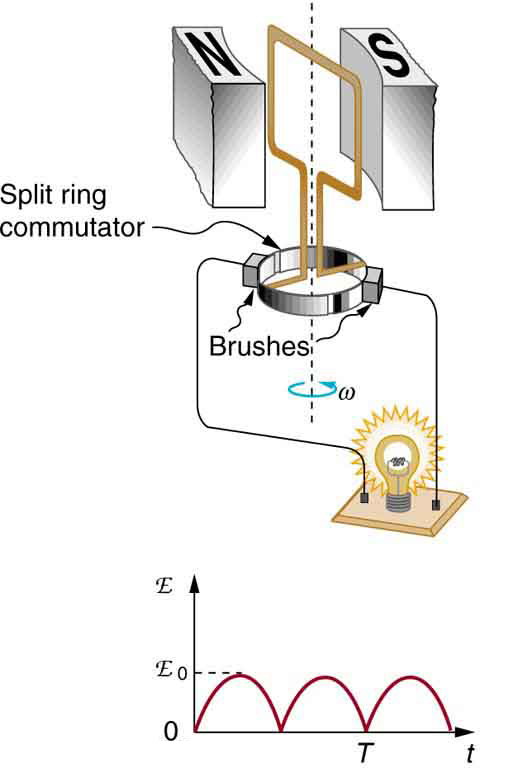
Figure 4 shows a scheme by which a generator can be made to produce pulsed DC. More elaborate arrangements of multiple coils and split rings can produce smoother DC, although electronic rather than mechanical means are usually used to make ripple-free DC.

Example 2: Calculating the Maximum Emf of a Generator

Calculate the maximum emf, $latex \boldsymbol{emf_0} $, of the generator that was the subject of Example 1.

Strategy

Once $latex \boldsymbol{\omega} $, the angular velocity, is determined, $latex \boldsymbol{emf_0 = NAB \omega} $ can be used to find $latex \boldsymbol{emf_0} $. All other quantities are known.

Solution

Angular velocity is defined to be the change in angle per unit time:

$latex \boldsymbol{\omega =} $ .

One-fourth of a revolution is $latex \boldsymbol{\pi / 2} $ radians, and the time is 0.0150 s; thus,

$latex \begin{array} {r @{{}={}} l} \boldsymbol{\omega} & \boldsymbol{\frac{\pi / 2 \;\textbf{rad}}{0.0150 \;\textbf{s}}} \\[1em] & \boldsymbol{104.7 \;\textbf{rad/s.}} \end{array} $

104.7 rad/s is exactly 1000 rpm. We substitute this value for $latex \boldsymbol{\omega} $ and the information from the previous example into $latex \boldsymbol{emf_0 = NAB \omega} $, yielding

$latex \begin{array}{r @{{}={}} l} \boldsymbol{emf_0} & \boldsymbol{NAB \omega} \\[1em] & \boldsymbol{200 (7.85 \times 10^{-3} \;\textbf{m}^2)(1.25 \;\textbf{T})(104.7 \;\textbf{rad/s}).} \\[1em] & \boldsymbol{206 \;\textbf{V}}. \end{array} $

Discussion

The maximum emf is greater than the average emf of 131 V found in the previous example, as it should be.

In real life, electric generators look a lot different than the figures in this section, but the principles are the same. The source of mechanical energy that turns the coil can be falling water (hydropower), steam produced by the burning of fossil fuels, or the kinetic energy of wind. Figure 5 shows a cutaway view of a steam turbine; steam moves over the blades connected to the shaft, which rotates the coil within the generator.

Generators illustrated in this section look very much like the motors illustrated previously. This is not coincidental. In fact, a motor becomes a generator when its shaft rotates. Certain early automobiles used their starter motor as a generator. In Chapter 23.6 Back Emf, we shall further explore the action of a motor as a generator.