200 25.3 The Law of Refraction
Summary
- Determine the index of refraction, given the speed of light in a medium.
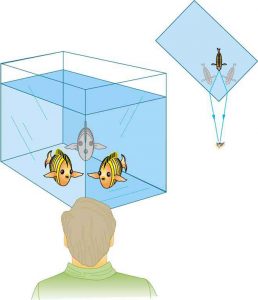
It is easy to notice some odd things when looking into a fish tank. For example, you may see the same fish appearing to be in two different places. (See Figure 1.) This is because light coming from the fish to us changes direction when it leaves the tank, and in this case, it can travel two different paths to get to our eyes. The changing of a light ray’s direction (loosely called bending) when it passes through variations in matter is called refraction. Refraction is responsible for a tremendous range of optical phenomena, from the action of lenses to voice transmission through optical fibers.
Refraction
The changing of a light ray’s direction (loosely called bending) when it passes through variations in matter is called refraction.
Speed of Light
The speed of light $latex \boldsymbol{c} $ not only affects refraction, it is one of the central concepts of Einstein’s theory of relativity. As the accuracy of the measurements of the speed of light were improved, $latex \boldsymbol{c} $ was found not to depend on the velocity of the source or the observer. However, the speed of light does vary in a precise manner with the material it traverses. These facts have far-reaching implications, as we will see in Chapter 28 Special Relativity. It makes connections between space and time and alters our expectations that all observers measure the same time for the same event, for example. The speed of light is so important that its value in a vacuum is one of the most fundamental constants in nature as well as being one of the four fundamental SI units.
Why does light change direction when passing from one material (medium) to another? It is because light changes speed when going from one material to another. So before we study the law of refraction, it is useful to discuss the speed of light and how it varies in different media.
The Speed of Light
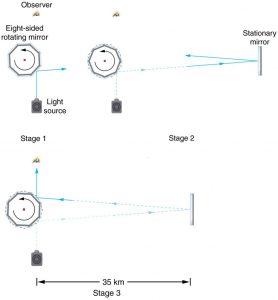
Early attempts to measure the speed of light, such as those made by Galileo, determined that light moved extremely fast, perhaps instantaneously. The first real evidence that light traveled at a finite speed came from the Danish astronomer Ole Roemer in the late 17th century. Roemer had noted that the average orbital period of one of Jupiter’s moons, as measured from Earth, varied depending on whether Earth was moving toward or away from Jupiter. He correctly concluded that the apparent change in period was due to the change in distance between Earth and Jupiter and the time it took light to travel this distance. From his 1676 data, a value of the speed of light was calculated to be $latex \boldsymbol{2.26 \times 10^8 \;\textbf{m/s}} $ (only 25% different from today’s accepted value). In more recent times, physicists have measured the speed of light in numerous ways and with increasing accuracy. One particularly direct method, used in 1887 by the American physicist Albert Michelson (1852–1931), is illustrated in Figure 2. Light reflected from a rotating set of mirrors was reflected from a stationary mirror 35 km away and returned to the rotating mirrors. The time for the light to travel can be determined by how fast the mirrors must rotate for the light to be returned to the observer’s eye.
The speed of light is now known to great precision. In fact, the speed of light in a vacuum $latex \boldsymbol{c} $ is so important that it is accepted as one of the basic physical quantities and has the fixed value
where the approximate value of $latex \boldsymbol{3.00 \times 10^8 \;\textbf{m/s}} $ is used whenever three-digit accuracy is sufficient. The speed of light through matter is less than it is in a vacuum, because light interacts with atoms in a material. The speed of light depends strongly on the type of material, since its interaction with different atoms, crystal lattices, and other substructures varies. We define the index of refraction $latex \boldsymbol{n} $ of a material to be
where $latex \boldsymbol{v} $ is the observed speed of light in the material. Since the speed of light is always less than $latex \boldsymbol{c} $ in matter and equals $latex \boldsymbol{c} $ only in a vacuum, the index of refraction is always greater than or equal to one.
Value of the Speed of Light
Index of Refraction
That is, $latex \boldsymbol{n \ge 1} $. Table 1 gives the indices of refraction for some representative substances. The values are listed for a particular wavelength of light, because they vary slightly with wavelength. (This can have important effects, such as colors produced by a prism.) Note that for gases, $latex \boldsymbol{n} $ is close to 1.0. This seems reasonable, since atoms in gases are widely separated and light travels at $latex \boldsymbol{c} $ in the vacuum between atoms. It is common to take $latex \boldsymbol{n = 1} $ for gases unless great precision is needed. Although the speed of light $latex \boldsymbol{v} $ in a medium varies considerably from its value $latex \boldsymbol{c} $ in a vacuum, it is still a large speed.
| Medium | n |
|---|---|
| Gases at 0ºC, 1 atm | |
| Air | 1.000293 |
| Carbon dioxide | 1.00045 |
| Hydrogen | 1.000139 |
| Oxygen | 1.000271 |
| Liquids at 20ºC | |
| Benzene | 1.501 |
| Carbon disulfide | 1.628 |
| Carbon tetrachloride | 1.461 |
| Ethanol | 1.361 |
| Glycerine | 1.473 |
| Water, fresh | 1.333 |
| Solids at 20ºC | |
| Diamond | 2.419 |
| Fluorite | 1.434 |
| Glass, crown | 1.52 |
| Glass, flint | 1.66 |
| Ice at 20ºC | 1.309 |
| Polystyrene | 1.49 |
| Plexiglas | 1.51 |
| Quartz, crystalline | 1.544 |
| Quartz, fused | 1.458 |
| Sodium chloride | 1.544 |
| Zircon | 1.923 |
| Table 1: Index of Refraction in Various Media | |
Example 1: Speed of Light in Matter
Calculate the speed of light in zircon, a material used in jewelry to imitate diamond.
Strategy
The speed of light in a material, $latex \boldsymbol{v} $, can be calculated from the index of refraction $latex \boldsymbol{n} $ of the material using the equation $latex \boldsymbol{n = c/v} $.
Solution
The equation for index of refraction states that $latex \boldsymbol{n=c/v} $. Rearranging this to determine $latex \boldsymbol{v} $ gives
The index of refraction for zircon is given as 1.923 in Table 1, and $latex \boldsymbol{c} $ is given in the equation for speed of light. Entering these values in the last expression gives
Discussion
This speed is slightly larger than half the speed of light in a vacuum and is still high compared with speeds we normally experience. The only substance listed in Table 1 that has a greater index of refraction than zircon is diamond. We shall see later that the large index of refraction for zircon makes it sparkle more than glass, but less than diamond.
Law of Refraction
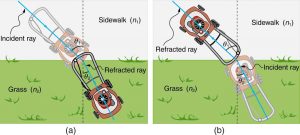
Figure 3 shows how a ray of light changes direction when it passes from one medium to another. As before, the angles are measured relative to a perpendicular to the surface at the point where the light ray crosses it. (Some of the incident light will be reflected from the surface, but for now we will concentrate on the light that is transmitted.) The change in direction of the light ray depends on how the speed of light changes. The change in the speed of light is related to the indices of refraction of the media involved. In the situations shown in Figure 3, medium 2 has a greater index of refraction than medium 1. This means that the speed of light is less in medium 2 than in medium 1. Note that as shown in Figure 3(a), the direction of the ray moves closer to the perpendicular when it slows down. Conversely, as shown in Figure 3(b), the direction of the ray moves away from the perpendicular when it speeds up. The path is exactly reversible. In both cases, you can imagine what happens by thinking about pushing a lawn mower from a footpath onto grass, and vice versa. Going from the footpath to grass, the front wheels are slowed and pulled to the side as shown. This is the same change in direction as for light when it goes from a fast medium to a slow one. When going from the grass to the footpath, the front wheels can move faster and the mower changes direction as shown. This, too, is the same change in direction as for light going from slow to fast.
The amount that a light ray changes its direction depends both on the incident angle and the amount that the speed changes. For a ray at a given incident angle, a large change in speed causes a large change in direction, and thus a large change in angle. The exact mathematical relationship is the law of refraction, or “Snell’s Law,” which is stated in equation form as
Here $latex \boldsymbol{n_1} $ and $latex \boldsymbol{n_2} $ are the indices of refraction for medium 1 and 2, and $latex \boldsymbol{\theta _1} $ and $latex \boldsymbol{\theta _2} $ are the angles between the rays and the perpendicular in medium 1 and 2, as shown in Figure 3. The incoming ray is called the incident ray and the outgoing ray the refracted ray, and the associated angles the incident angle and the refracted angle. The law of refraction is also called Snell’s law after the Dutch mathematician Willebrord Snell (1591–1626), who discovered it in 1621. Snell’s experiments showed that the law of refraction was obeyed and that a characteristic index of refraction $latex \boldsymbol{n} $ could be assigned to a given medium. Snell was not aware that the speed of light varied in different media, but through experiments he was able to determine indices of refraction from the way light rays changed direction.
The Law of Refraction
Take-Home Experiment: A Broken Pencil
A classic observation of refraction occurs when a pencil is placed in a glass half filled with water. Do this and observe the shape of the pencil when you look at the pencil sideways, that is, through air, glass, water. Explain your observations. Draw ray diagrams for the situation.
Example 2: Determine the Index of Refraction from Refraction Data
Find the index of refraction for medium 2 in Figure 3(a), assuming medium 1 is air and given the incident angle is $latex \boldsymbol{30.0 ^{\circ}} $ and the angle of refraction is
$latex \boldsymbol{22.0 ^{\circ}} $.
Strategy
The index of refraction for air is taken to be 1 in most cases (and up to four significant figures, it is 1.000). Thus $latex \boldsymbol{n_1 = 1.00} $ here. From the given information, $latex \boldsymbol{\theta _1 = 30.0^{\circ}} $ and $latex \boldsymbol{\theta _2 = 22.0 ^{\circ}} $. With this information, the only unknown in Snell’s law is $latex \boldsymbol{n_2} $, so that it can be used to find this unknown.
Solution
Snell’s law is
Rearranging to isolate $latex \boldsymbol{n_2} $ gives
Entering known values,
Discussion
This is the index of refraction for water, and Snell could have determined it by measuring the angles and performing this calculation. He would then have found 1.33 to be the appropriate index of refraction for water in all other situations, such as when a ray passes from water to glass. Today we can verify that the index of refraction is related to the speed of light in a medium by measuring that speed directly.
Example 3: A Larger Change in Direction
Suppose that in a situation like that in Example 2, light goes from air to diamond and that the incident angle is $latex \boldsymbol{30.0 ^{\circ}} $. Calculate the angle of refraction $latex \boldsymbol{\theta _2} $ in the diamond.
Strategy
Again the index of refraction for air is taken to be $latex \boldsymbol{n_1 = 1.00} $, and we are given $latex \boldsymbol{\theta _1 = 30.0 ^{\circ}} $. We can look up the index of refraction for diamond in Table 1, finding $latex \boldsymbol{n_2 = 2.419} $. The only unknown in Snell’s law is $latex \boldsymbol{\theta _2} $, which we wish to determine.
Solution
Solving Snell’s law for $latex \boldsymbol{\textbf{sin} \;\theta _2} $ yields
Entering known values,
The angle is thus
Discussion
For the same $latex \boldsymbol{30^{\circ}} $ angle of incidence, the angle of refraction in diamond is significantly smaller than in water ($latex \boldsymbol{11.9^{\circ}} $ rather than $latex \boldsymbol{22^{\circ}} $ —see the preceding example). This means there is a larger change in direction in diamond. The cause of a large change in direction is a large change in the index of refraction (or speed). In general, the larger the change in speed, the greater the effect on the direction of the ray.
Section Summary
- The changing of a light ray’s direction when it passes through variations in matter is called refraction.
- The speed of light in vacuum $latex \boldsymbol{c = 2.9972458 \times 10^8 \;\textbf{m/s} \approx 3.00 \times 10^8 \;\textbf{m/s}} $.
- Index of refraction $latex \boldsymbol{n = \frac{c}{v}} $, where $latex \boldsymbol{v} $ is the speed of light in the material, $latex \boldsymbol{c} $ is the speed of light in vacuum, and $latex \boldsymbol{n} $ is the index of refraction.
- Snell’s law, the law of refraction, is stated in equation form as $latex \boldsymbol{n_1 \;\textbf{sin} \;\theta _1 = n_2 \;\textbf{sin} \;\theta _2} $.
Conceptual Questions
1: Diffusion by reflection from a rough surface is described in this chapter. Light can also be diffused by refraction. Describe how this occurs in a specific situation, such as light interacting with crushed ice.
2: Why is the index of refraction always greater than or equal to 1?
3: Does the fact that the light flash from lightning reaches you before its sound prove that the speed of light is extremely large or simply that it is greater than the speed of sound? Discuss how you could use this effect to get an estimate of the speed of light.
4: Will light change direction toward or away from the perpendicular when it goes from air to water? Water to glass? Glass to air?
5: Explain why an object in water always appears to be at a depth shallower than it actually is? Why do people sometimes sustain neck and spinal injuries when diving into unfamiliar ponds or waters?
6: Explain why a person’s legs appear very short when wading in a pool. Justify your explanation with a ray diagram showing the path of rays from the feet to the eye of an observer who is out of the water.
8: Suppose light were incident from air onto a material that had a negative index of refraction, say –1.3; where does the refracted light ray go?
Problems & Exercises
1: What is the speed of light in water? In glycerine?
2: What is the speed of light in air? In crown glass?
3: Calculate the index of refraction for a medium in which the speed of light is $latex \boldsymbol{2.012 \times 10^8 \;\textbf{m/s}} $, and identify the most likely substance based on Table 1.
4: In what substance in Table 1 is the speed of light $latex \boldsymbol{2.290 \times 10^8 \;\textbf{m/s}} $?
5: There was a major collision of an asteroid with the Moon in medieval times. It was described by monks at Canterbury Cathedral in England as a red glow on and around the Moon. How long after the asteroid hit the Moon, which is $latex \boldsymbol{3.84 \times 10^5 \;\textbf{km}} $ away, would the light first arrive on Earth?
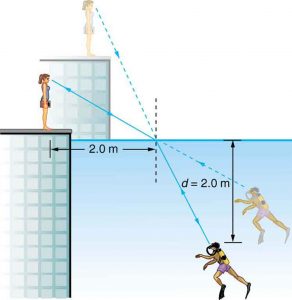
6: A scuba diver training in a pool looks at his instructor as shown in Figure 5. What angle does the ray from the instructor’s face make with the perpendicular to the water at the point where the ray enters? The angle between the ray in the water and the perpendicular to the water is $latex \boldsymbol{25.0^{\circ}} $.
7: Components of some computers communicate with each other through optical fibers having an index of refraction $latex \boldsymbol{n = 1.55} $. What time in nanoseconds is required for a signal to travel 0.200 m through such a fiber?
8: (a) Using information in Figure 5, find the height of the instructor’s head above the water, noting that you will first have to calculate the angle of incidence. (b) Find the apparent depth of the diver’s head below water as seen by the instructor.
9: Suppose you have an unknown clear substance immersed in water, and you wish to identify it by finding its index of refraction. You arrange to have a beam of light enter it at an angle of $latex \boldsymbol{45.0^{\circ}} $, and you observe the angle of refraction to be $latex \boldsymbol{40.3^{\circ}} $. What is the index of refraction of the substance and its likely identity?
10: On the Moon’s surface, lunar astronauts placed a corner reflector, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. What percent correction is needed to account for the delay in time due to the slowing of light in Earth’s atmosphere? Assume the distance to the Moon is precisely $latex \boldsymbol{3.84 \times 10^8 \;\textbf{m}} $, and Earth’s atmosphere (which varies in density with altitude) is equivalent to a layer 30.0 km thick with a constant index of refraction $latex \boldsymbol{n=1.000293} $.
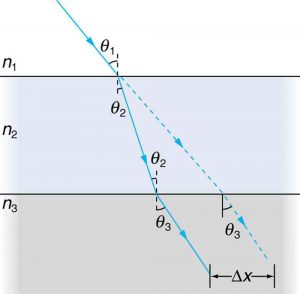
11: Suppose Figure 6 represents a ray of light going from air through crown glass into water, such as going into a fish tank. Calculate the amount the ray is displaced by the glass ($latex \boldsymbol{\Delta x} $), given that the incident angle is $latex \boldsymbol{40.0^{\circ}} $ and the glass is 1.00 cm thick.
12: Figure 6 shows a ray of light passing from one medium into a second and then a third. Show that $latex \boldsymbol{\theta _3} $ is the same as it would be if the second medium were not present (provided total internal reflection does not occur).
13: Unreasonable Results
Suppose light travels from water to another substance, with an angle of incidence of $latex \boldsymbol{10.0^{\circ}} $ and an angle of refraction of $latex \boldsymbol{14.9^{\circ}} $. (a) What is the index of refraction of the other substance? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
14: Construct Your Own Problem
Consider sunlight entering the Earth’s atmosphere at sunrise and sunset—that is, at a $latex \boldsymbol{90^{\circ}} $ incident angle. Taking the boundary between nearly empty space and the atmosphere to be sudden, calculate the angle of refraction for sunlight. This lengthens the time the Sun appears to be above the horizon, both at sunrise and sunset. Now construct a problem in which you determine the angle of refraction for different models of the atmosphere, such as various layers of varying density. Your instructor may wish to guide you on the level of complexity to consider and on how the index of refraction varies with air density.
15: Unreasonable Results
Light traveling from water to a gemstone strikes the surface at an angle of $latex \boldsymbol{80.0 ^{\circ}} $ and has an angle of refraction of $latex \boldsymbol{15.2^{\circ}} $. (a) What is the speed of light in the gemstone? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Glossary
- refraction
- changing of a light ray’s direction when it passes through variations in matter
- index of refraction
- for a material, the ratio of the speed of light in vacuum to that in the material
Solutions
Problems & Exercises
1: $latex \boldsymbol{2.25 \times 10^8 \;\textbf{m/s}} $ in water
$latex \boldsymbol{2.04 \times 10^8 \;\textbf{m/s}} $ in glycerine
3: $latex \boldsymbol{1.490} $ , polystyrene
5: $latex \boldsymbol{1.28 \;\textbf{s}} $
7: $latex \boldsymbol{1.03 \;\textbf{ns}} $
13: (a) 0.898
(b) Can’t have $latex \boldsymbol{n < 1.00} $ since this would imply a speed greater than $latex \boldsymbol{c} $.
(c) Refracted angle is too big relative to the angle of incidence.
15: (a) $latex \boldsymbol{\frac{c}{5.00}} $
(b) Speed of light too slow, since index is much greater than that of diamond.
(c) Angle of refraction is unreasonable relative to the angle of incidence.