273 34.2 General Relativity and Quantum Gravity
Summary
- Explain the effect of gravity on light.
- Discuss black hole.
- Explain quantum gravity.
When we talk of black holes or the unification of forces, we are actually discussing aspects of general relativity and quantum gravity. We know from Chapter 28 Special Relativity that relativity is the study of how different observers measure the same event, particularly if they move relative to one another. Einstein’s theory of general relativity describes all types of relative motion including accelerated motion and the effects of gravity. General relativity encompasses special relativity and classical relativity in situations where acceleration is zero and relative velocity is small compared with the speed of light. Many aspects of general relativity have been verified experimentally, some of which are better than science fiction in that they are bizarre but true. Quantum gravity is the theory that deals with particle exchange of gravitons as the mechanism for the force, and with extreme conditions where quantum mechanics and general relativity must both be used. A good theory of quantum gravity does not yet exist, but one will be needed to understand how all four forces may be unified. If we are successful, the theory of quantum gravity will encompass all others, from classical physics to relativity to quantum mechanics—truly a Theory of Everything (TOE).
General Relativity
Einstein first considered the case of no observer acceleration when he developed the revolutionary special theory of relativity, publishing his first work on it in 1905. By 1916, he had laid the foundation of general relativity, again almost on his own. Much of what Einstein did to develop his ideas was to mentally analyze certain carefully and clearly defined situations—doing this is to perform a thought experiment. Figure 1 illustrates a thought experiment like the ones that convinced Einstein that light must fall in a gravitational field. Think about what a person feels in an elevator that is accelerated upward. It is identical to being in a stationary elevator in a gravitational field. The feet of a person are pressed against the floor, and objects released from hand fall with identical accelerations. In fact, it is not possible, without looking outside, to know what is happening—acceleration upward or gravity. This led Einstein to correctly postulate that acceleration and gravity will produce identical effects in all situations. So, if acceleration affects light, then gravity will, too. Figure 1 shows the effect of acceleration on a beam of light shone horizontally at one wall. Since the accelerated elevator moves up during the time light travels across the elevator, the beam of light strikes low, seeming to the person to bend down. (Normally a tiny effect, since the speed of light is so great.) The same effect must occur due to gravity, Einstein reasoned, since there is no way to tell the effects of gravity acting downward from acceleration of the elevator upward. Thus gravity affects the path of light, even though we think of gravity as acting between masses and photons are massless.
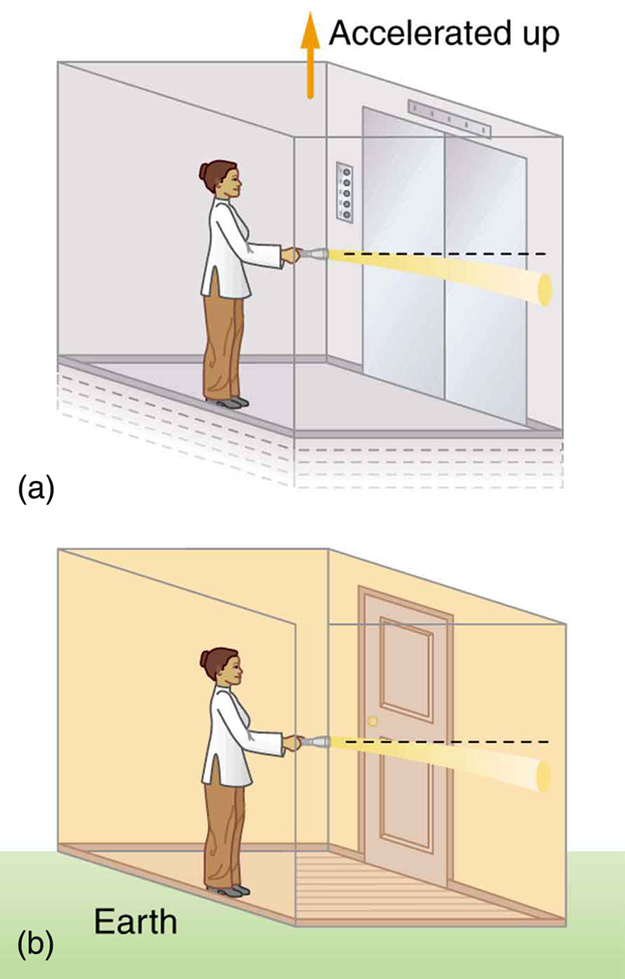
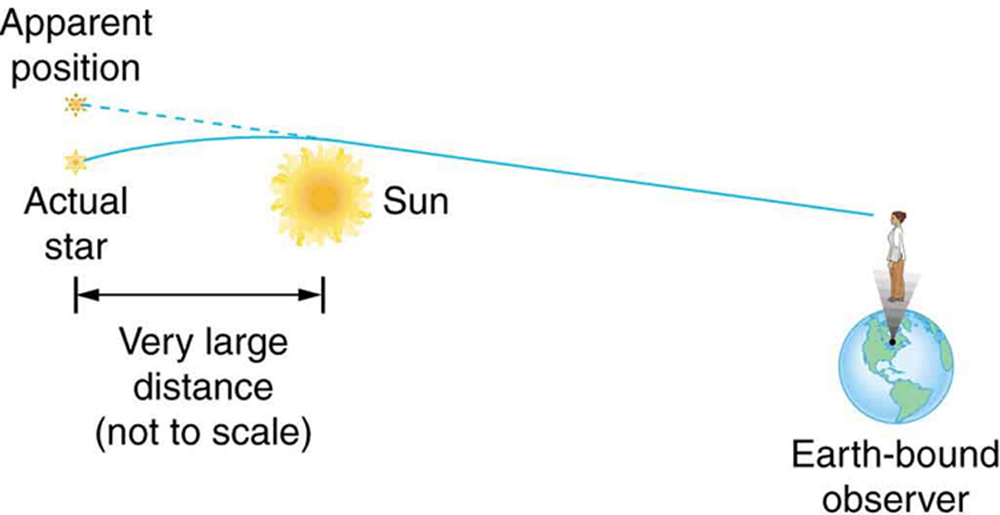
Einstein’s theory of general relativity got its first verification in 1919 when starlight passing near the Sun was observed during a solar eclipse. (See Figure 2.) During an eclipse, the sky is darkened and we can briefly see stars. Those in a line of sight nearest the Sun should have a shift in their apparent positions. Not only was this shift observed, but it agreed with Einstein’s predictions well within experimental uncertainties. This discovery created a scientific and public sensation. Einstein was now a folk hero as well as a very great scientist. The bending of light by matter is equivalent to a bending of space itself, with light following the curve. This is another radical change in our concept of space and time. It is also another connection that any particle with mass or energy (massless photons) is affected by gravity.
There are several current forefront efforts related to general relativity. One is the observation and analysis of gravitational lensing of light. Another is analysis of the definitive proof of the existence of black holes. Direct observation of gravitational waves or moving wrinkles in space is being searched for. Theoretical efforts are also being aimed at the possibility of time travel and wormholes into other parts of space due to black holes.
Gravitational lensing
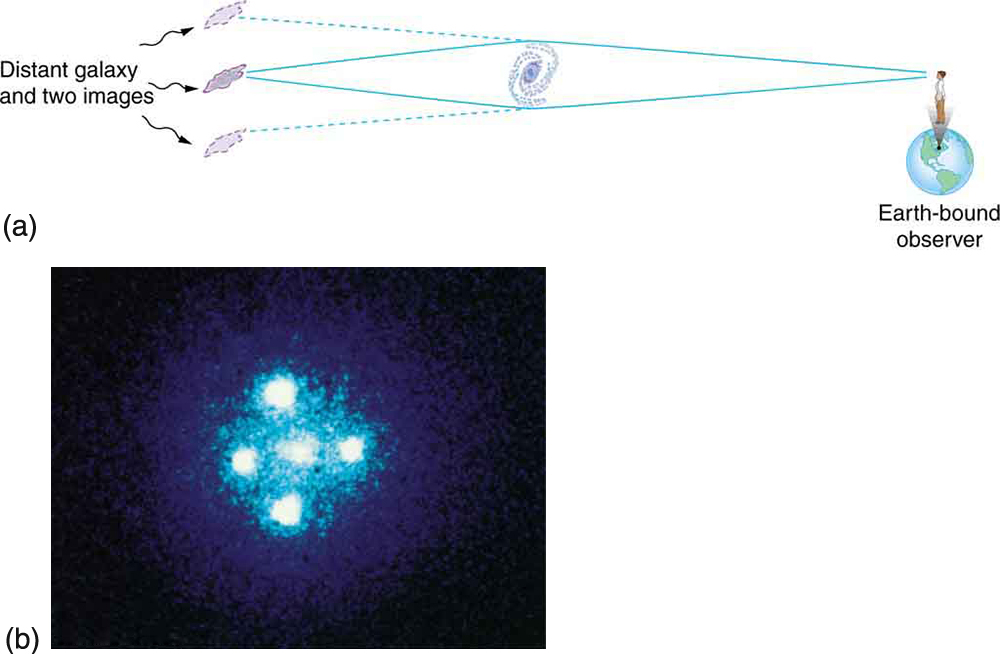
As you can see in Figure 2, light is bent toward a mass, producing an effect much like a converging lens (large masses are needed to produce observable effects). On a galactic scale, the light from a distant galaxy could be “lensed” into several images when passing close by another galaxy on its way to Earth. Einstein predicted this effect, but he considered it unlikely that we would ever observe it. A number of cases of this effect have now been observed; one is shown in Figure 3. This effect is a much larger scale verification of general relativity. But such gravitational lensing is also useful in verifying that the red shift is proportional to distance. The red shift of the intervening galaxy is always less than that of the one being lensed, and each image of the lensed galaxy has the same red shift. This verification supplies more evidence that red shift is proportional to distance. Confidence that the multiple images are not different objects is bolstered by the observations that if one image varies in brightness over time, the others also vary in the same manner.
Black holes
Black holes are objects having such large gravitational fields that things can fall in, but nothing, not even light, can escape. Bodies, like the Earth or the Sun, have what is called an escape velocity. If an object moves straight up from the body, starting at the escape velocity, it will just be able to escape the gravity of the body. The greater the acceleration of gravity on the body, the greater is the escape velocity. As long ago as the late 1700s, it was proposed that if the escape velocity is greater than the speed of light, then light cannot escape. Simon Laplace (1749–1827), the French astronomer and mathematician, even incorporated this idea of a dark star into his writings. But the idea was dropped after Young’s double slit experiment showed light to be a wave. For some time, light was thought not to have particle characteristics and, thus, could not be acted upon by gravity. The idea of a black hole was very quickly reincarnated in 1916 after Einstein’s theory of general relativity was published. It is now thought that black holes can form in the supernova collapse of a massive star, forming an object perhaps 10 km across and having a mass greater than that of our Sun. It is interesting that several prominent physicists who worked on the concept, including Einstein, firmly believed that nature would find a way to prohibit such objects.
Black holes are difficult to observe directly, because they are small and no light comes directly from them. In fact, no light comes from inside the event horizon, which is defined to be at a distance from the object at which the escape velocity is exactly the speed of light. The radius of the event horizon is known as the Schwarzschild radius $latex \boldsymbol{R_S} $ and is given by
where $latex \boldsymbol{G} $ is the universal gravitational constant, $latex \boldsymbol{M} $ is the mass of the body, and $latex \boldsymbol{c} $ is the speed of light. The event horizon is the edge of the black hole and $latex \boldsymbol{R_S} $ is its radius (that is, the size of a black hole is twice $latex \boldsymbol{R_S} $). Since $latex \boldsymbol{G} $ is small and $latex \boldsymbol{c^2} $ is large, you can see that black holes are extremely small, only a few kilometers for masses a little greater than the Sun’s. The object itself is inside the event horizon.
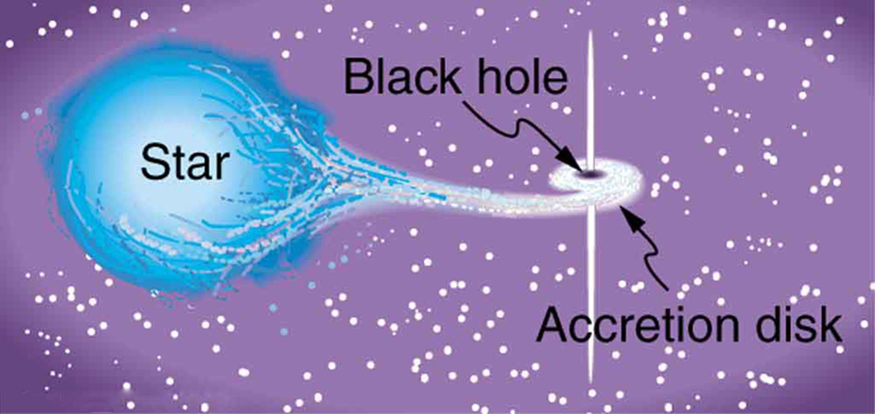
Physics near a black hole is fascinating. Gravity increases so rapidly that, as you approach a black hole, the tidal effects tear matter apart, with matter closer to the hole being pulled in with much more force than that only slightly farther away. This can pull a companion star apart and heat inflowing gases to the point of producing X rays. (See Figure 4.) We have observed X rays from certain binary star systems that are consistent with such a picture. This is not quite proof of black holes, because the X rays could also be caused by matter falling onto a neutron star. These objects were first discovered in 1967 by the British astrophysicists, Jocelyn Bell and Anthony Hewish. Neutron stars are literally a star composed of neutrons. They are formed by the collapse of a star’s core in a supernova, during which electrons and protons are forced together to form neutrons (the reverse of neutron $latex \boldsymbol{\beta} $ decay). Neutron stars are slightly larger than a black hole of the same mass and will not collapse further because of resistance by the strong force. However, neutron stars cannot have a mass greater than about eight solar masses or they must collapse to a black hole. With recent improvements in our ability to resolve small details, such as with the orbiting Chandra X-ray Observatory, it has become possible to measure the masses of X-ray-emitting objects by observing the motion of companion stars and other matter in their vicinity. What has emerged is a plethora of X-ray-emitting objects too massive to be neutron stars. This evidence is considered conclusive and the existence of black holes is widely accepted. These black holes are concentrated near galactic centers.
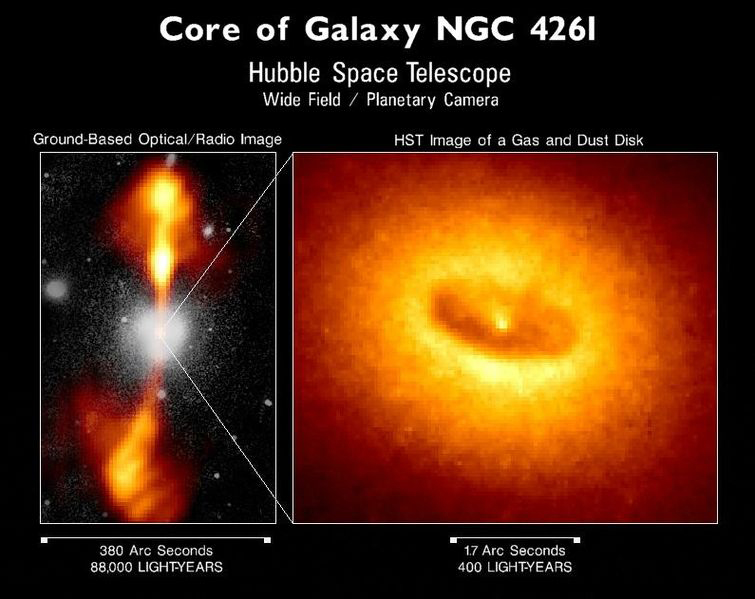
We also have evidence that supermassive black holes may exist at the cores of many galaxies, including the Milky Way. Such a black hole might have a mass millions or even billions of times that of the Sun, and it would probably have formed when matter first coalesced into a galaxy billions of years ago. Supporting this is the fact that very distant galaxies are more likely to have abnormally energetic cores. Some of the moderately distant galaxies, and hence among the younger, are known as quasars and emit as much or more energy than a normal galaxy but from a region less than a light year across. Quasar energy outputs may vary in times less than a year, so that the energy-emitting region must be less than a light year across. The best explanation of quasars is that they are young galaxies with a supermassive black hole forming at their core, and that they become less energetic over billions of years. In closer superactive galaxies, we observe tremendous amounts of energy being emitted from very small regions of space, consistent with stars falling into a black hole at the rate of one or more a month. The Hubble Space Telescope (1994) observed an accretion disk in the galaxy M87 rotating rapidly around a region of extreme energy emission. (See Figure 4.) A jet of material being ejected perpendicular to the plane of rotation gives further evidence of a supermassive black hole as the engine.
Gravitational waves
If a massive object distorts the space around it, like the foot of a water bug on the surface of a pond, then movement of the massive object should create waves in space like those on a pond. Gravitational waves are mass-created distortions in space that propagate at the speed of light and are predicted by general relativity. Since gravity is by far the weakest force, extreme conditions are needed to generate significant gravitational waves. Gravity near binary neutron star systems is so great that significant gravitational wave energy is radiated as the two neutron stars orbit one another. American astronomers, Joseph Taylor and Russell Hulse, measured changes in the orbit of such a binary neutron star system. They found its orbit to change precisely as predicted by general relativity, a strong indication of gravitational waves, and were awarded the 1993 Nobel Prize. But direct detection of gravitational waves on Earth would be conclusive. For many years, various attempts have been made to detect gravitational waves by observing vibrations induced in matter distorted by these waves. American physicist Joseph Weber pioneered this field in the 1960s, but no conclusive events have been observed. (No gravity wave detectors were in operation at the time of the 1987A supernova, unfortunately.) There are now several ambitious systems of gravitational wave detectors in use around the world. These include the LIGO (Laser Interferometer Gravitational Wave Observatory) system with two laser interferometer detectors, one in the state of Washington and another in Louisiana (See Figure 6) and the VIRGO (Variability of Irradiance and Gravitational Oscillations) facility in Italy with a single detector.
Quantum Gravity
Black holes radiate
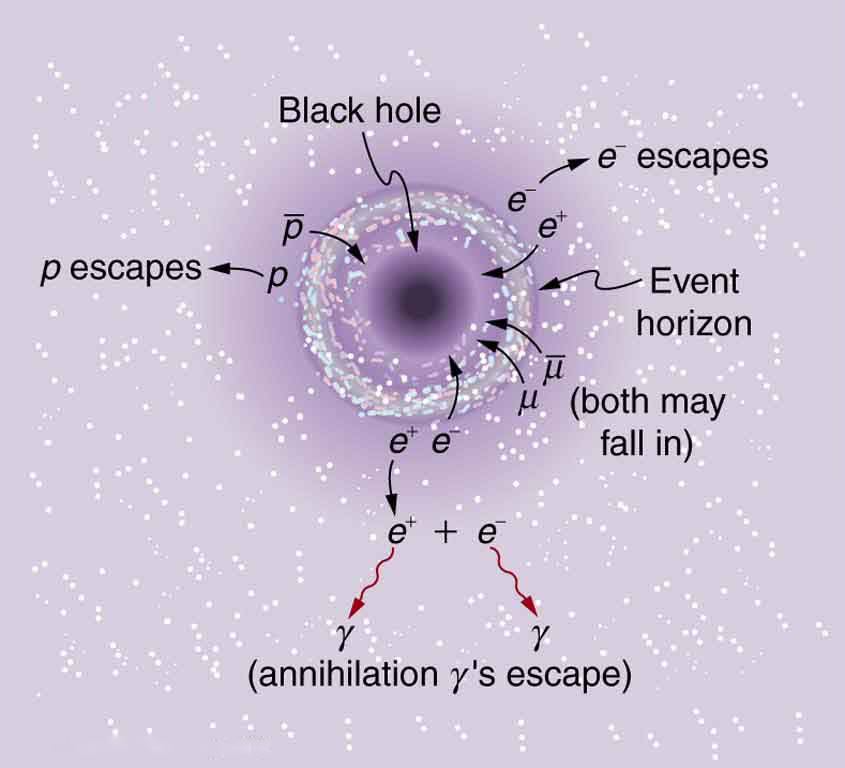
Quantum gravity is important in those situations where gravity is so extremely strong that it has effects on the quantum scale, where the other forces are ordinarily much stronger. The early universe was such a place, but black holes are another. The first significant connection between gravity and quantum effects was made by the Russian physicist Yakov Zel’dovich in 1971, and other significant advances followed from the British physicist Stephen Hawking. (See Figure 7.) These two showed that black holes could radiate away energy by quantum effects just outside the event horizon (nothing can escape from inside the event horizon). Black holes are, thus, expected to radiate energy and shrink to nothing, although extremely slowly for most black holes. The mechanism is the creation of a particle-antiparticle pair from energy in the extremely strong gravitational field near the event horizon. One member of the pair falls into the hole and the other escapes, conserving momentum. (See Figure 8.) When a black hole loses energy and, hence, rest mass, its event horizon shrinks, creating an even greater gravitational field. This increases the rate of pair production so that the process grows exponentially until the black hole is nuclear in size. A final burst of particles and $latex \boldsymbol{\gamma} $ rays ensues. This is an extremely slow process for black holes about the mass of the Sun (produced by supernovas) or larger ones (like those thought to be at galactic centers), taking on the order of $latex \boldsymbol{10^{67}} $ years or longer! Smaller black holes would evaporate faster, but they are only speculated to exist as remnants of the Big Bang. Searches for characteristic $latex \boldsymbol{\gamma} $ -ray bursts have produced events attributable to more mundane objects like neutron stars accreting matter.

Wormholes and time travel
The subject of time travel captures the imagination. Theoretical physicists, such as the American Kip Thorne, have treated the subject seriously, looking into the possibility that falling into a black hole could result in popping up in another time and place—a trip through a so-called wormhole. Time travel and wormholes appear in innumerable science fiction dramatizations, but the consensus is that time travel is not possible in theory. While still debated, it appears that quantum gravity effects inside a black hole prevent time travel due to the creation of particle pairs. Direct evidence is elusive.
The shortest time
Theoretical studies indicate that, at extremely high energies and correspondingly early in the universe, quantum fluctuations may make time intervals meaningful only down to some finite time limit. Early work indicated that this might be the case for times as long as $latex \boldsymbol{10^{-43} \;\textbf{s}} $, the time at which all forces were unified. If so, then it would be meaningless to consider the universe at times earlier than this. Subsequent studies indicate that the crucial time may be as short as $latex \boldsymbol{10^{-95} \;\textbf{s}} $. But the point remains—quantum gravity seems to imply that there is no such thing as a vanishingly short time. Time may, in fact, be grainy with no meaning to time intervals shorter than some tiny but finite size.
The future of quantum gravity
Not only is quantum gravity in its infancy, no one knows how to get started on a theory of gravitons and unification of forces. The energies at which TOE should be valid may be so high (at least $latex \boldsymbol{10^{19} \;\textbf{GeV}} $) and the necessary particle separation so small (less than $latex \boldsymbol{10^{-35} \;\textbf{m}} $) that only indirect evidence can provide clues. For some time, the common lament of theoretical physicists was one so familiar to struggling students—how do you even get started? But Hawking and others have made a start, and the approach many theorists have taken is called Superstring theory, the topic of the Chapter 34.3 Superstrings.
Section Summary
- Einstein’s theory of general relativity includes accelerated frames and, thus, encompasses special relativity and gravity. Created by use of careful thought experiments, it has been repeatedly verified by real experiments.
- One direct result of this behavior of nature is the gravitational lensing of light by massive objects, such as galaxies, also seen in the microlensing of light by smaller bodies in our galaxy.
- Another prediction is the existence of black holes, objects for which the escape velocity is greater than the speed of light and from which nothing can escape.
- The event horizon is the distance from the object at which the escape velocity equals the speed of light $latex \boldsymbol{c} $. It is called the Schwarzschild radius $latex \boldsymbol{R_S} $ and is given by
- where $latex \boldsymbol{G} $ is the universal gravitational constant, and $latex \boldsymbol{M} $ is the mass of the body.
- Physics is unknown inside the event horizon, and the possibility of wormholes and time travel are being studied.
- Candidates for black holes may power the extremely energetic emissions of quasars, distant objects that seem to be early stages of galactic evolution.
- Neutron stars are stellar remnants, having the density of a nucleus, that hint that black holes could form from supernovas, too.
- Gravitational waves are wrinkles in space, predicted by general relativity but not yet observed, caused by changes in very massive objects.
- Quantum gravity is an incompletely developed theory that strives to include general relativity, quantum mechanics, and unification of forces (thus, a TOE).
- One unconfirmed connection between general relativity and quantum mechanics is the prediction of characteristic radiation from just outside black holes.
Conceptual Questions
1: Quantum gravity, if developed, would be an improvement on both general relativity and quantum mechanics, but more mathematically difficult. Under what circumstances would it be necessary to use quantum gravity? Similarly, under what circumstances could general relativity be used? When could special relativity, quantum mechanics, or classical physics be used?
2: Does observed gravitational lensing correspond to a converging or diverging lens? Explain briefly.
3: Suppose you measure the red shifts of all the images produced by gravitational lensing, such as in Figure 3.You find that the central image has a red shift less than the outer images, and those all have the same red shift. Discuss how this not only shows that the images are of the same object, but also implies that the red shift is not affected by taking different paths through space. Does it imply that cosmological red shifts are not caused by traveling through space (light getting tired, perhaps)?
4: What are gravitational waves, and have they yet been observed either directly or indirectly?
5: Is the event horizon of a black hole the actual physical surface of the object?
6: Suppose black holes radiate their mass away and the lifetime of a black hole created by a supernova is about $latex \boldsymbol{10^{67}} $ years. How does this lifetime compare with the accepted age of the universe? Is it surprising that we do not observe the predicted characteristic radiation?
Problems & Exercises
1: What is the Schwarzschild radius of a black hole that has a mass eight times that of our Sun? Note that stars must be more massive than the Sun to form black holes as a result of a supernova.
2: Black holes with masses smaller than those formed in supernovas may have been created in the Big Bang. Calculate the radius of one that has a mass equal to the Earth’s.
3: Supermassive black holes are thought to exist at the center of many galaxies.
(a) What is the radius of such an object if it has a mass of $latex \boldsymbol{10^9} $ Suns?
(b) What is this radius in light years?
4: Construct Your Own Problem
Consider a supermassive black hole near the center of a galaxy. Calculate the radius of such an object based on its mass. You must consider how much mass is reasonable for these large objects, and which is now nearly directly observed. (Information on black holes posted on the Web by NASA and other agencies is reliable, for example.)
Glossary
- black holes
- objects having such large gravitational fields that things can fall in, but nothing, not even light, can escape
- general relativity
- Einstein’s theory that describes all types of relative motion including accelerated motion and the effects of gravity
- gravitational waves
- mass-created distortions in space that propagate at the speed of light and that are predicted by general relativity
- escape velocity
- takeoff velocity when kinetic energy just cancels gravitational potential energy
- event horizon
- the distance from the object at which the escape velocity is exactly the speed of light
- neutron stars
- literally a star composed of neutrons
- Schwarzschild radius
- the radius of the event horizon
- thought experiment
- mental analysis of certain carefully and clearly defined situations to develop an idea
- quasars
- the moderately distant galaxies that emit as much or more energy than a normal galaxy
- Quantum gravity
- the theory that deals with particle exchange of gravitons as the mechanism for the force
Solutions
Problems & Exercises
1: 23.6 km
3: (a) $latex \boldsymbol{2.95 \times 10^{12} \;\textbf{m}} $
(b) $latex \boldsymbol{3.12 \times 10^{-4} \;\textbf{ly}} $

