261 32.5 Fusion
Summary
- Define nuclear fusion.
- Discuss processes to achieve practical fusion energy generation.
While basking in the warmth of the summer sun, a student reads of the latest breakthrough in achieving sustained thermonuclear power and vaguely recalls hearing about the cold fusion controversy. The three are connected. The Sun’s energy is produced by nuclear fusion (see Figure 1). Thermonuclear power is the name given to the use of controlled nuclear fusion as an energy source. While research in the area of thermonuclear power is progressing, high temperatures and containment difficulties remain. The cold fusion controversy centered around unsubstantiated claims of practical fusion power at room temperatures.

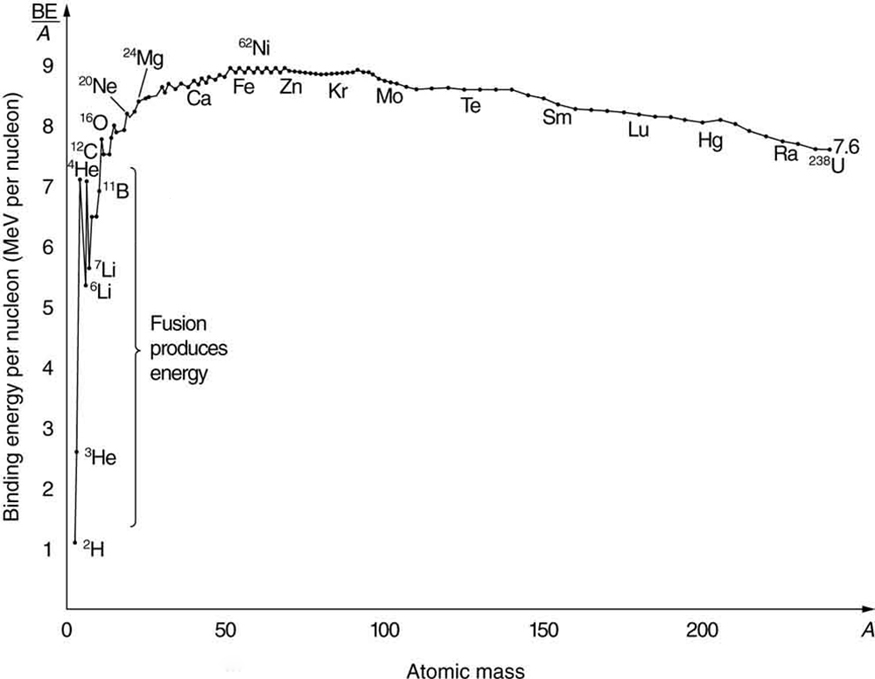
Nuclear fusion is a reaction in which two nuclei are combined, or fused, to form a larger nucleus. We know that all nuclei have less mass than the sum of the masses of the protons and neutrons that form them. The missing mass times $latex \boldsymbol{c^2} $ equals the binding energy of the nucleus—the greater the binding energy, the greater the missing mass. We also know that $latex \boldsymbol{\textbf{BE/}A} $ , the binding energy per nucleon, is greater for medium-mass nuclei and has a maximum at Fe (iron). This means that if two low-mass nuclei can be fused together to form a larger nucleus, energy can be released. The larger nucleus has a greater binding energy and less mass per nucleon than the two that combined. Thus mass is destroyed in the fusion reaction, and energy is released (see Figure 2). On average, fusion of low-mass nuclei releases energy, but the details depend on the actual nuclides involved.
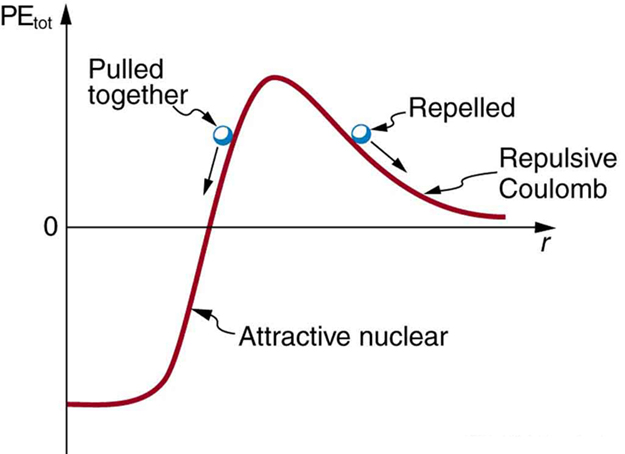
The major obstruction to fusion is the Coulomb repulsion between nuclei. Since the attractive nuclear force that can fuse nuclei together is short ranged, the repulsion of like positive charges must be overcome to get nuclei close enough to induce fusion. Figure 3 shows an approximate graph of the potential energy between two nuclei as a function of the distance between their centers. The graph is analogous to a hill with a well in its center. A ball rolled from the right must have enough kinetic energy to get over the hump before it falls into the deeper well with a net gain in energy. So it is with fusion. If the nuclei are given enough kinetic energy to overcome the electric potential energy due to repulsion, then they can combine, release energy, and fall into a deep well. One way to accomplish this is to heat fusion fuel to high temperatures so that the kinetic energy of thermal motion is sufficient to get the nuclei together.
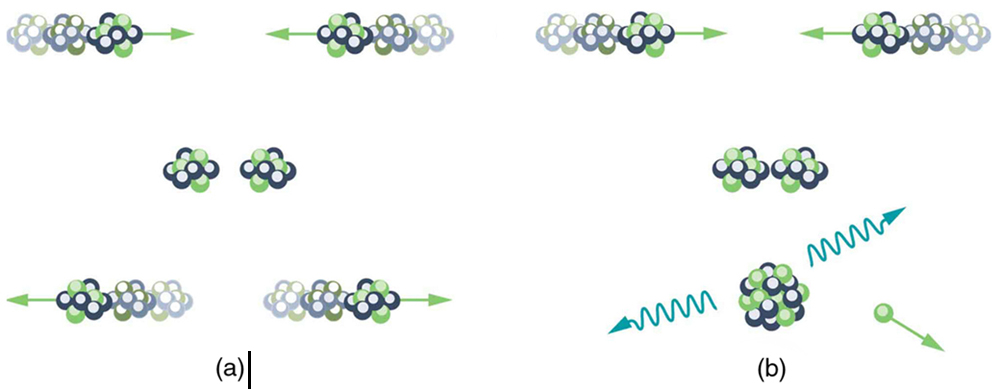
You might think that, in the core of our Sun, nuclei are coming into contact and fusing. However, in fact, temperatures on the order of $latex \boldsymbol{^{108} \textbf{K}} $ are needed to actually get the nuclei in contact, exceeding the core temperature of the Sun. Quantum mechanical tunneling is what makes fusion in the Sun possible, and tunneling is an important process in most other practical applications of fusion, too. Since the probability of tunneling is extremely sensitive to barrier height and width, increasing the temperature greatly increases the rate of fusion. The closer reactants get to one another, the more likely they are to fuse (see Figure 4). Thus most fusion in the Sun and other stars takes place at their centers, where temperatures are highest. Moreover, high temperature is needed for thermonuclear power to be a practical source of energy.
The Sun produces energy by fusing protons or hydrogen nuclei $latex \boldsymbol{^1 \textbf{H}} $ (by far the Sun’s most abundant nuclide) into helium nuclei $latex \boldsymbol{^4 \textbf{He}} $. The principal sequence of fusion reactions forms what is called the proton-proton cycle:
where $latex \boldsymbol{e ^+} $ stands for a positron and $latex \boldsymbol{v_e} $ is an electron neutrino. (The energy in parentheses is released by the reaction.) Note that the first two reactions must occur twice for the third to be possible, so that the cycle consumes six protons ( $latex \boldsymbol{^1 \textbf{H}} $ ) but gives back two. Furthermore, the two positrons produced will find two electrons and annihilate to form four more $latex \boldsymbol{\gamma} $ rays, for a total of six. The overall effect of the cycle is thus
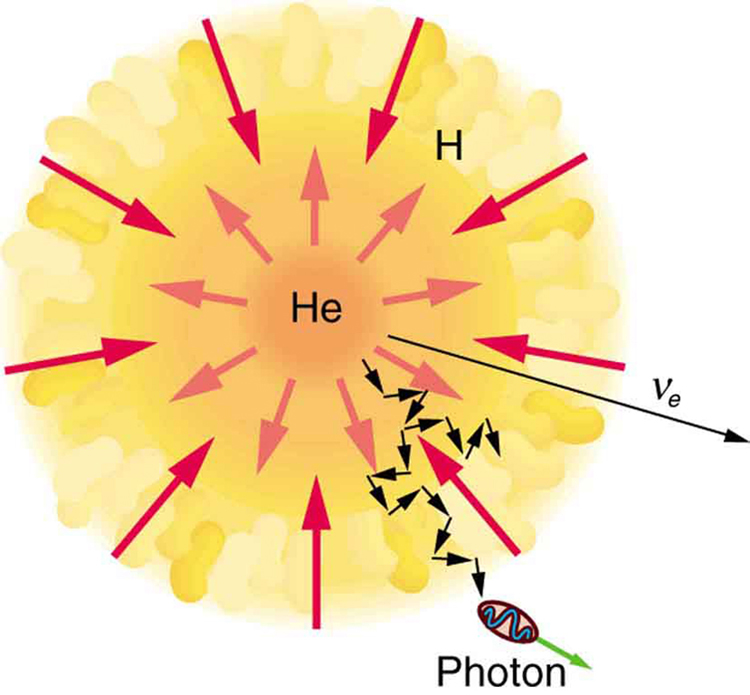
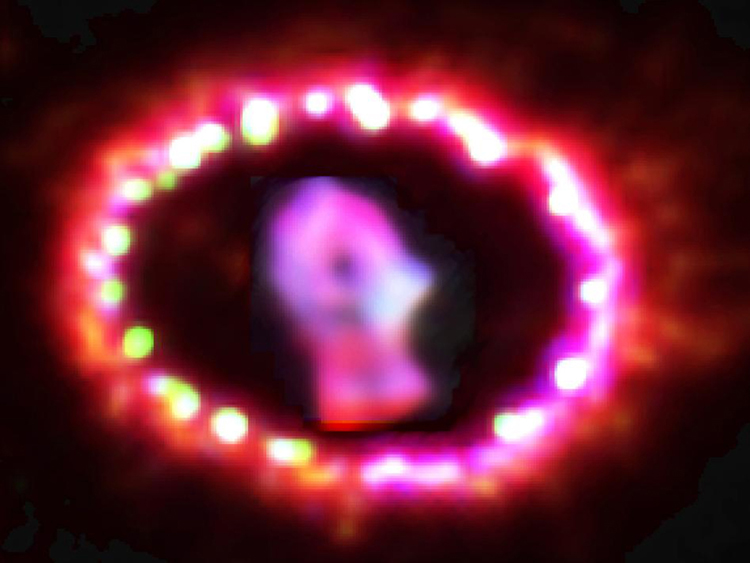
Theories of the proton-proton cycle (and other energy-producing cycles in stars) were pioneered by the German-born, American physicist Hans Bethe (1906–2005), starting in 1938. He was awarded the 1967 Nobel Prize in physics for this work, and he has made many other contributions to physics and society. Neutrinos produced in these cycles escape so readily that they provide us an excellent means to test these theories and study stellar interiors. Detectors have been constructed and operated for more than four decades now to measure solar neutrinos (see Figure 6). Although solar neutrinos are detected and neutrinos were observed from Supernova 1987A (Figure 7), too few solar neutrinos were observed to be consistent with predictions of solar energy production. After many years, this solar neutrino problem was resolved with a blend of theory and experiment that showed that the neutrino does indeed have mass. It was also found that there are three types of neutrinos, each associated with a different type of nuclear decay.

The proton-proton cycle is not a practical source of energy on Earth, in spite of the great abundance of hydrogen ($latex \boldsymbol{^1 \textbf{H}} $). The reaction $latex \boldsymbol{{^1 \textbf{H}} + {^1 \textbf{H}} \rightarrow {^2 \textbf{H}} + e^+ + v_e} $ has a very low probability of occurring. (This is why our Sun will last for about ten billion years.) However, a number of other fusion reactions are easier to induce. Among them are:
Deuterium ($latex \boldsymbol{^2 \textbf{H}} $) is about 0.015% of natural hydrogen, so there is an immense amount of it in sea water alone. In addition to an abundance of deuterium fuel, these fusion reactions produce large energies per reaction (in parentheses), but they do not produce much radioactive waste. Tritium ($latex \boldsymbol{^3 \textbf{H}} $) is radioactive, but it is consumed as a fuel (the reaction $latex \boldsymbol{{^2 \textbf{H}} + {^3 \textbf{H}} \rightarrow {^4 \textbf{He}} + n} $), and the neutrons and $latex \boldsymbol{\gamma} $ s can be shielded. The neutrons produced can also be used to create more energy and fuel in reactions like
and
Note that these last two reactions, and $latex \boldsymbol{{^2 \textbf{H}} + {^2 \textbf{H}} \rightarrow {^4 \textbf{He}} + \gamma} $, put most of their energy output into the $latex \boldsymbol{\gamma} $ ray, and such energy is difficult to utilize.
The three keys to practical fusion energy generation are to achieve the temperatures necessary to make the reactions likely, to raise the density of the fuel, and to confine it long enough to produce large amounts of energy. These three factors—temperature, density, and time—complement one another, and so a deficiency in one can be compensated for by the others. Ignition is defined to occur when the reactions produce enough energy to be self-sustaining after external energy input is cut off. This goal, which must be reached before commercial plants can be a reality, has not been achieved. Another milestone, called break-even, occurs when the fusion power produced equals the heating power input. Break-even has nearly been reached and gives hope that ignition and commercial plants may become a reality in a few decades.
Two techniques have shown considerable promise. The first of these is called magnetic confinement and uses the property that charged particles have difficulty crossing magnetic field lines. The tokamak, shown in Figure 8, has shown particular promise. The tokamak’s toroidal coil confines charged particles into a circular path with a helical twist due to the circulating ions themselves. In 1995, the Tokamak Fusion Test Reactor at Princeton in the US achieved world-record plasma temperatures as high as 500 million degrees Celsius. This facility operated between 1982 and 1997. A joint international effort is underway in France to build a tokamak-type reactor that will be the stepping stone to commercial power. ITER, as it is called, will be a full-scale device that aims to demonstrate the feasibility of fusion energy. It will generate 500 MW of power for extended periods of time and will achieve break-even conditions. It will study plasmas in conditions similar to those expected in a fusion power plant. Completion is scheduled for 2018.

The second promising technique aims multiple lasers at tiny fuel pellets filled with a mixture of deuterium and tritium. Huge power input heats the fuel, evaporating the confining pellet and crushing the fuel to high density with the expanding hot plasma produced. This technique is called inertial confinement, because the fuel’s inertia prevents it from escaping before significant fusion can take place. Higher densities have been reached than with tokamaks, but with smaller confinement times. In 2009, the Lawrence Livermore Laboratory (CA) completed a laser fusion device with 192 ultraviolet laser beams that are focused upon a D-T pellet (see Figure 9).

Example 1: Calculating Energy and Power from Fusion
(a) Calculate the energy released by the fusion of a 1.00-kg mixture of deuterium and tritium, which produces helium. There are equal numbers of deuterium and tritium nuclei in the mixture.
(b) If this takes place continuously over a period of a year, what is the average power output?
Strategy
According to $latex \boldsymbol{{^2 \textbf{H}} + {^3 \textbf{H}} \rightarrow {^4 \textbf{He}} + n} $, the energy per reaction is 17.59 MeV. To find the total energy released, we must find the number of deuterium and tritium atoms in a kilogram. Deuterium has an atomic mass of about 2 and tritium has an atomic mass of about 3, for a total of about 5 g per mole of reactants or about 200 mol in 1.00 kg. To get a more precise figure, we will use the atomic masses from Appendix A. The power output is best expressed in watts, and so the energy output needs to be calculated in joules and then divided by the number of seconds in a year.
Solution for (a)
The atomic mass of deuterium ($latex \boldsymbol{^2 \textbf{H}} $) is 2.014102 u, while that of tritium ($latex \boldsymbol{^3 \textbf{H}} $) is 3.016049 u, for a total of 5.032151 u per reaction. So a mole of reactants has a mass of 5.03 g, and in 1.00 kg there are $latex \boldsymbol{(1000 \;\textbf{g})/(5.03 \;\textbf{g/mol}) = 198.8 \;\textbf{mol of reactants}} $. The number of reactions that take place is therefore
The total energy output is the number of reactions times the energy per reaction:
Solution for (b)
Power is energy per unit time. One year has $latex \boldsymbol{3.16 \times 10^7 \;\textbf{s}} $, so
Discussion
By now we expect nuclear processes to yield large amounts of energy, and we are not disappointed here. The energy output of $latex \boldsymbol{3.37 \times 10^{14} \;\textbf{J}} $ from fusing 1.00 kg of deuterium and tritium is equivalent to 2.6 million gallons of gasoline and about eight times the energy output of the bomb that destroyed Hiroshima. Yet the average backyard swimming pool has about 6 kg of deuterium in it, so that fuel is plentiful if it can be utilized in a controlled manner. The average power output over a year is more than 10 MW, impressive but a bit small for a commercial power plant. About 32 times this power output would allow generation of 100 MW of electricity, assuming an efficiency of one-third in converting the fusion energy to electrical energy.
Section Summary
- Nuclear fusion is a reaction in which two nuclei are combined to form a larger nucleus. It releases energy when light nuclei are fused to form medium-mass nuclei.
- Fusion is the source of energy in stars, with the proton-proton cycle,
$latex \begin{array} {r @{{} \rightarrow{}} l @{{} \;\;\; {}} l} \boldsymbol{^1 \textbf{H} + {^1 \textbf{H}}} & \boldsymbol{{^2 \textbf{H}} + e ^+ + v_e} & \boldsymbol{(0.42 \;\textbf{MeV})} \\[1em] \boldsymbol{{^1 \textbf{H}} + {^2 \textbf{H}}} & \boldsymbol{{^3 \textbf{He}} + \gamma} & \boldsymbol{(5.49 \;\textbf{MeV})} \\[1em] \boldsymbol{{^3 \textbf{He}} + {^3 \textbf{He}}} & \boldsymbol{{^4 \textbf{He}} + {^1 \textbf{H}} + {^1 \textbf{H}}} & \boldsymbol{(12.86 \textbf{MeV})} \end{array} $
being the principal sequence of energy-producing reactions in our Sun.
- The overall effect of the proton-proton cycle is
$latex \begin{array} {r @{{} \rightarrow {}}l @{{} \;\;\; {}} l} \boldsymbol{{2e ^-} + 4 {^1 \textbf{H}}} & \boldsymbol{{^4 \textbf{He}} + {2v_e} + {6 \gamma}} & \boldsymbol{(26.7 \;\textbf{MeV})} \end{array} $
where the 26.7 MeV includes the energy of the positrons emitted and annihilated.
- Attempts to utilize controlled fusion as an energy source on Earth are related to deuterium and tritium, and the reactions play important roles.
- Ignition is the condition under which controlled fusion is self-sustaining; it has not yet been achieved. Break-even, in which the fusion energy output is as great as the external energy input, has nearly been achieved.
- Magnetic confinement and inertial confinement are the two methods being developed for heating fuel to sufficiently high temperatures, at sufficient density, and for sufficiently long times to achieve ignition. The first method uses magnetic fields and the second method uses the momentum of impinging laser beams for confinement.
Conceptual Questions
1: Why does the fusion of light nuclei into heavier nuclei release energy?
2: Energy input is required to fuse medium-mass nuclei, such as iron or cobalt, into more massive nuclei. Explain why.
3: In considering potential fusion reactions, what is the advantage of the reaction $latex \boldsymbol{{^2 \textbf{H}} + {^3 \textbf{H}} \rightarrow {^4 \textbf{He}} + n} $ over the reaction $latex \boldsymbol{{^2 \textbf{H}}+{^2 \textbf{H}} \rightarrow {^3 \textbf{He}} +n} $ ?
4: Give reasons justifying the contention made in the text that energy from the fusion reaction $latex \boldsymbol{{^2 \textbf{H}} + {^2 \textbf{H}} \rightarrow {^4 \textbf{He}} + \gamma} $ is relatively difficult to capture and utilize.
Problems & Exercises
1: Verify that the total number of nucleons, total charge, and electron family number are conserved for each of the fusion reactions in the proton-proton cycle in
and
(List the value of each of the conserved quantities before and after each of the reactions.)
2: Calculate the energy output in each of the fusion reactions in the proton-proton cycle, and verify the values given in the above summary.
3: Show that the total energy released in the proton-proton cycle is 26.7 MeV, considering the overall effect in $latex \boldsymbol{{^1 \textbf{H}} + {^1 \textbf{H}} \rightarrow {^2 \textbf{H}} + e^+ + v_e} $, $latex \boldsymbol{^1 \textbf{H} + {^2 \textbf{H}} \rightarrow {^3 \textbf{He} + \gamma} } $ , and $latex \boldsymbol{{^3 \textbf{He}} + {^3 \textbf{He}} \rightarrow {^4 \textbf{He}} + {^1 \textbf{H}} + {^1 \textbf{H}}} $ and being certain to include the annihilation energy.
4: Verify by listing the number of nucleons, total charge, and electron family number before and after the cycle that these quantities are conserved in the overall proton-proton cycle in $latex \boldsymbol{2e-+ 4 {^1 \textbf{H}} \rightarrow {^4 \textbf{He}} + 2v_{\textbf{e}} + 6 \gamma} $.
5: The energy produced by the fusion of a 1.00-kg mixture of deuterium and tritium was found in Example Example 1 – Calculating Energy and Power from Fusion. Approximately how many kilograms would be required to supply the annual energy use in the United States?
6: Tritium is naturally rare, but can be produced by the reaction $latex \boldsymbol{n + {^2 \textbf{H}} \rightarrow {^3 \textbf{H}} + \gamma} $. How much energy in MeV is released in this neutron capture?
7: Two fusion reactions mentioned in the text are
$latex \boldsymbol{n + {^3 \textbf{He}} \rightarrow {^4 \textbf{He}} + \gamma} $
and
$latex \boldsymbol{n+ {^1 \textbf{H}} \rightarrow {^2 \textbf{H}}+ \gamma} $.
Both reactions release energy, but the second also creates more fuel. Confirm that the energies produced in the reactions are 20.58 and 2.22 MeV, respectively. Comment on which product nuclide is most tightly bound, $latex \boldsymbol{^4 \textbf{He}} $ or $latex \boldsymbol{^2 \textbf{H}} $.
8: (a) Calculate the number of grams of deuterium in an 80,000-L swimming pool, given deuterium is 0.0150% of natural hydrogen.
(b) Find the energy released in joules if this deuterium is fused via the reaction $latex \boldsymbol{{^2 \textbf{H}} + {^2 \textbf{H}} \rightarrow {^3 \textbf{He}} + n} $.
(c) Could the neutrons be used to create more energy?
(d) Discuss the amount of this type of energy in a swimming pool as compared to that in, say, a gallon of gasoline, also taking into consideration that water is far more abundant.
9: How many kilograms of water are needed to obtain the 198.8 mol of deuterium, assuming that deuterium is 0.01500% (by number) of natural hydrogen?
10: The power output of the Sun is $latex \boldsymbol{4 \times 10^{26} \;\textbf{W}} $.
(a) If 90% of this is supplied by the proton-proton cycle, how many protons are consumed per second?
(b) How many neutrinos per second should there be per square meter at the Earth from this process? This huge number is indicative of how rarely a neutrino interacts, since large detectors observe very few per day.
Another set of reactions that result in the fusing of hydrogen into helium in the Sun and especially in hotter stars is called the carbon cycle. It is
11: Write down the overall effect of the carbon cycle (as was done for the proton-proton cycle in $latex \boldsymbol{2e^- + ^{41} \textbf{H} \rightarrow ^4 \textbf{He} + 2v_e + 6 \gamma} $ ). Note the number of protons ( $latex \boldsymbol{^1 \textbf{H}} $) required and assume that the positrons (
$latex \boldsymbol{e^+} $) annihilate electrons to form more $latex \boldsymbol{\gamma} $ rays.
12: (a) Find the total energy released in MeV in each carbon cycle (elaborated in the above problem) including the annihilation energy.
(b) How does this compare with the proton-proton cycle output?
13: Verify that the total number of nucleons, total charge, and electron family number are conserved for each of the fusion reactions in the carbon cycle given in the above problem. (List the value of each of the conserved quantities before and after each of the reactions.)
14: Integrated Concepts
The laser system tested for inertial confinement can produce a 100-kJ pulse only 1.00 ns in duration. (a) What is the power output of the laser system during the brief pulse?
(b) How many photons are in the pulse, given their wavelength is $latex \boldsymbol{1.06 \;\mu \textbf{m}} $ ?
(c) What is the total momentum of all these photons?
(d) How does the total photon momentum compare with that of a single 1.00 MeV deuterium nucleus?
15: Integrated Concepts
Find the amount of energy given to the $latex \boldsymbol{^4 \textbf{He}} $ nucleus and to the $latex \boldsymbol{\gamma} $ ray in the reaction $latex \boldsymbol{n + {^{3} \textbf{He}} \rightarrow {^{4} \textbf{He}} + \gamma} $ , using the conservation of momentum principle and taking the reactants to be initially at rest. This should confirm the contention that most of the energy goes to the $latex \boldsymbol{\gamma} $ ray.
16: Integrated Concepts
(a) What temperature gas would have atoms moving fast enough to bring two $latex \boldsymbol{^3 \textbf{He}} $ nuclei into contact? Note that, because both are moving, the average kinetic energy only needs to be half the electric potential energy of these doubly charged nuclei when just in contact with one another.
(b) Does this high temperature imply practical difficulties for doing this in controlled fusion?
17: Integrated Concepts
(a) Estimate the years that the deuterium fuel in the oceans could supply the energy needs of the world. Assume world energy consumption to be ten times that of the United States which is $latex \boldsymbol{8 \times 10^{19}} $ J/y and that the deuterium in the oceans could be converted to energy with an efficiency of 32%. You must estimate or look up the amount of water in the oceans and take the deuterium content to be 0.015% of natural hydrogen to find the mass of deuterium available. Note that approximate energy yield of deuterium is $latex \boldsymbol{3.37 \times 10^{14}} $ J/kg.
(b) Comment on how much time this is by any human measure. (It is not an unreasonable result, only an impressive one.)
Glossary
- break-even
- when fusion power produced equals the heating power input
- ignition
- when a fusion reaction produces enough energy to be self-sustaining after external energy input is cut off
- inertial confinement
- a technique that aims multiple lasers at tiny fuel pellets evaporating and crushing them to high density
- magnetic confinement
- a technique in which charged particles are trapped in a small region because of difficulty in crossing magnetic field lines
- nuclear fusion
- a reaction in which two nuclei are combined, or fused, to form a larger nucleus
- proton-proton cycle
- the combined reactions $latex \boldsymbol{{^1 \textbf{H}} + {^1 \textbf{H}} \rightarrow {^2 \textbf{H}} + e^+ + v_e} $, and $latex \boldsymbol{{^3 \textbf{He}} + {^3 \textbf{He}} \rightarrow {^4 \textbf{He}} + {^1 \textbf{H}} + {^1 \textbf{H}}} $
Solutions
Problems & Exercises
1: (a) $latex \boldsymbol{A = 1+1=2} $ , $latex \boldsymbol{Z=1+1=1+1} $ , $latex \boldsymbol{\textbf{efn}=0= -1+1} $
(b) $latex \boldsymbol{A=1+2=3} $ , $latex \boldsymbol{Z=1+1=2} $ , $latex \boldsymbol{\textbf{efn}=0=0} $
(c) $latex \boldsymbol{A = 3+3=4+1+1} $ , $latex \boldsymbol{Z=2+2=2+1+1} $ , $latex \boldsymbol{\textbf{efn}=0=0} $
3: $latex \begin{array}{r @{{}={}} l} \boldsymbol{E} & \boldsymbol{(m_{\textbf{i}} – m_{\textbf{f}})c^2} \\[1em] & \boldsymbol{[4m (1\textbf{H}) – m(4 \textbf{He})]c^2} \\[1em] & \boldsymbol{[4(1.007825) – 4.002603](931.5 \;\textbf{MeV})} \\[1em] & \boldsymbol{26.73 \;\textbf{MeV}} \end{array} $
5: $latex \boldsymbol{3.12 \times 10^5 \;\textbf{kg}} $ (about 200 tons)
7:
$latex \begin{array}{r @{{}={}} l} \boldsymbol{E} & \boldsymbol{(m_{\textbf{i}} – m_{\textbf{f}})c^2} \\[1em] \boldsymbol{E_1} & \boldsymbol{ (1.008665 + 3.016030 – 4.002603)(931.5 \;\textbf{MeV})} \\[1em] & \boldsymbol{20.58 \;\textbf{MeV}} \\[1em] \boldsymbol{E_2} & \boldsymbol{(1.008665 + 1.007825 – 2.014102)(931.5 \;\textbf{MeV})} \\[1em] & \boldsymbol{2.224 \;\textbf{MeV}} \end{array} $
$latex \boldsymbol{^4 \textbf{He}} $ is more tightly bound, since this reaction gives off more energy per nucleon.
9: $latex \boldsymbol{1.19 \times 10^4 \;\textbf{kg}} $
$latex \boldsymbol{2e^- + ^{41} \textbf{H} \rightarrow ^4 \textbf{He} + 7 \gamma +2v_e} $
13: (a) $latex \boldsymbol{A=12+1=13} $ , $latex \boldsymbol{Z=6+1=7} $ , $latex \boldsymbol{\textbf{efn}=0=0} $
(b) $latex \boldsymbol{A=13=13} $ , $latex \boldsymbol{Z=7=6+1} $ , $latex \boldsymbol{\textbf{efn}=0=-1+1} $
(c) $latex \boldsymbol{A=13+1=14} $ , $latex \boldsymbol{Z=6+1=7} $ , $latex \boldsymbol{\textbf{efn}=0=0} $
(d) $latex \boldsymbol{A=14+1=15} $ , $latex \boldsymbol{Z=7+1=8} $ , $latex \boldsymbol{\textbf{efn}=0=0} $
(e) $latex \boldsymbol{A=15=15} $ , $latex \boldsymbol{Z=8=7+1} $ , $latex \boldsymbol{\textbf{efn}=0=-1+1} $
(f) $latex \boldsymbol{A=15+1=12+4} $ , $latex \boldsymbol{Z=7+1=6+2} $ , $latex \boldsymbol{\textbf{efn} = 0 = 0} $
15: $latex \boldsymbol{E_{\gamma} = 20.6 \;\textbf{MeV}} $
$latex \boldsymbol{E_{^4 \textbf{He}} = 5.68 \times 10^{-2} \;\textbf{MeV}} $
(a) $latex \boldsymbol{3 \times 10^9 \;\textbf{y}} $
(b) This is approximately half the lifetime of the Earth.

