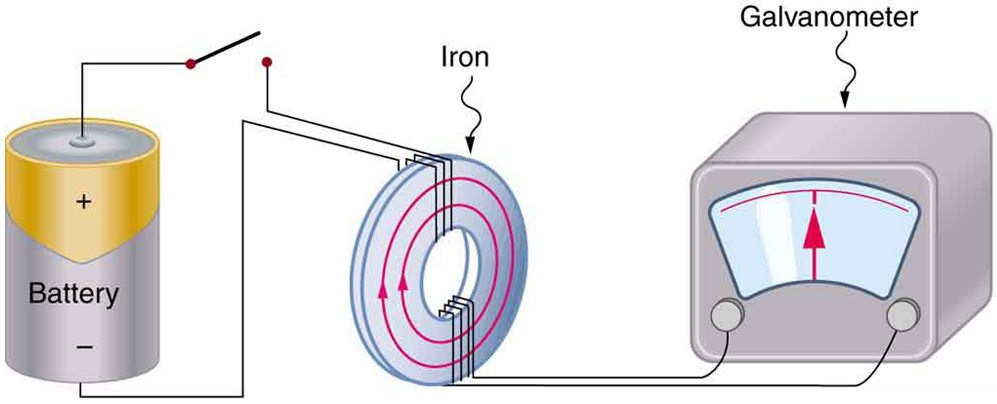
The apparatus used by Faraday to demonstrate that magnetic fields can create currents is illustrated in Figure 1. When the switch is closed, a magnetic field is produced in the coil on the top part of the iron ring and transmitted to the coil on the bottom part of the ring. The galvanometer is used to detect any current induced in the coil on the bottom. It was found that each time the switch is closed, the galvanometer detects a current in one direction in the coil on the bottom. (You can also observe this in a physics lab.) Each time the switch is opened, the galvanometer detects a current in the opposite direction. Interestingly, if the switch remains closed or open for any length of time, there is no current through the galvanometer. Closing and opening the switch induces the current. It is the change in magnetic field that creates the current. More basic than the current that flows is the emfthat causes it. The current is a result of an emf induced by a changing magnetic field, whether or not there is a path for current to flow.

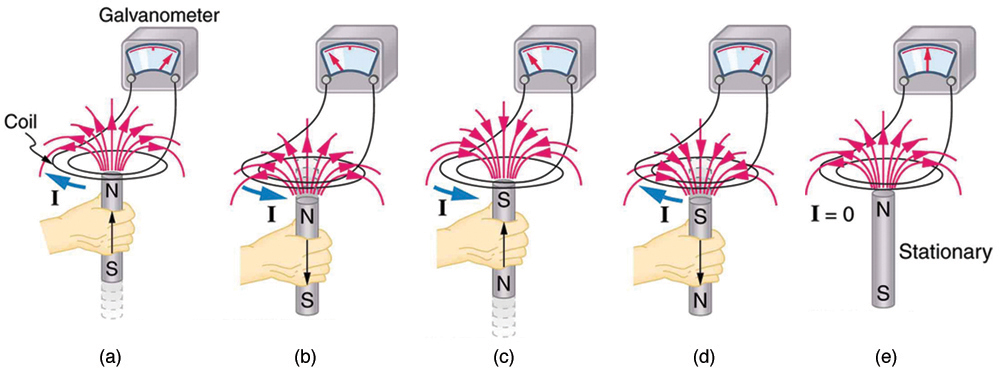
An experiment easily performed and often done in physics labs is illustrated in Figure 2. An emf is induced in the coil when a bar magnet is pushed in and out of it. Emfs of opposite signs are produced by motion in opposite directions, and the emfs are also reversed by reversing poles. The same results are produced if the coil is moved rather than the magnet—it is the relative motion that is important. The faster the motion, the greater the emf, and there is no emf when the magnet is stationary relative to the coil.

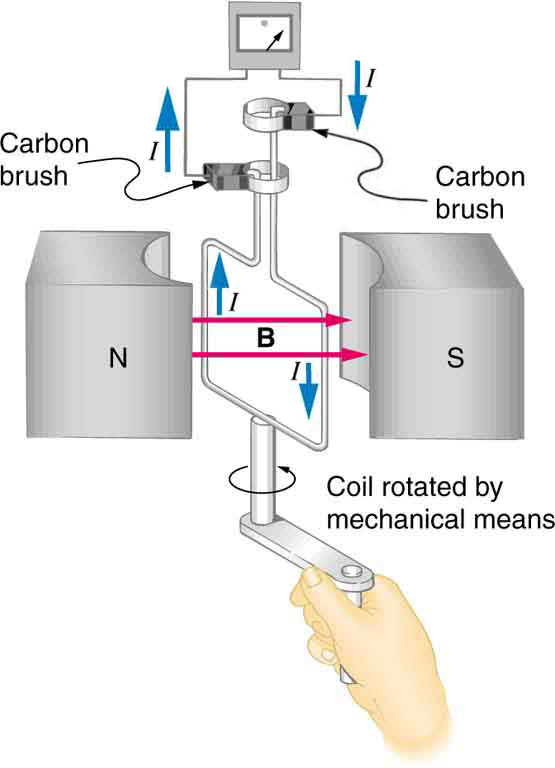
The method of inducing an emf used in most electric generators is shown in Figure 3. A coil is rotated in a magnetic field, producing an alternating current emf, which depends on rotation rate and other factors that will be explored in later sections. Note that the generator is remarkably similar in construction to a motor (another symmetry).

So we see that changing the magnitude or direction of a magnetic field produces an emf. Experiments revealed that there is a crucial quantity called the magnetic flux, $latex \boldsymbol{\phi} $ , given by

where $latex \boldsymbol{B} $ is the magnetic field strength over an area $latex \boldsymbol{A} $, at an angle $latex \boldsymbol{\theta} $ with the perpendicular to the area as shown in Figure 4. Any change in magnetic flux $latex \boldsymbol{\phi} $ induces an emf. This process is defined to be electromagnetic induction. Units of magnetic flux $latex \boldsymbol{\phi} $ are $latex \boldsymbol{\textbf{T} \cdot \textbf{m}^2} $. As seen in Figure 4, $latex \boldsymbol{B \;\textbf{cos} \;\theta = B_{\perp}} $, which is the component of $latex \boldsymbol{B} $ perpendicular to the area $latex \boldsymbol{A} $. Thus magnetic flux is $latex \boldsymbol{\phi = B_{\perp} A} $, the product of the area and the component of the magnetic field perpendicular to it.

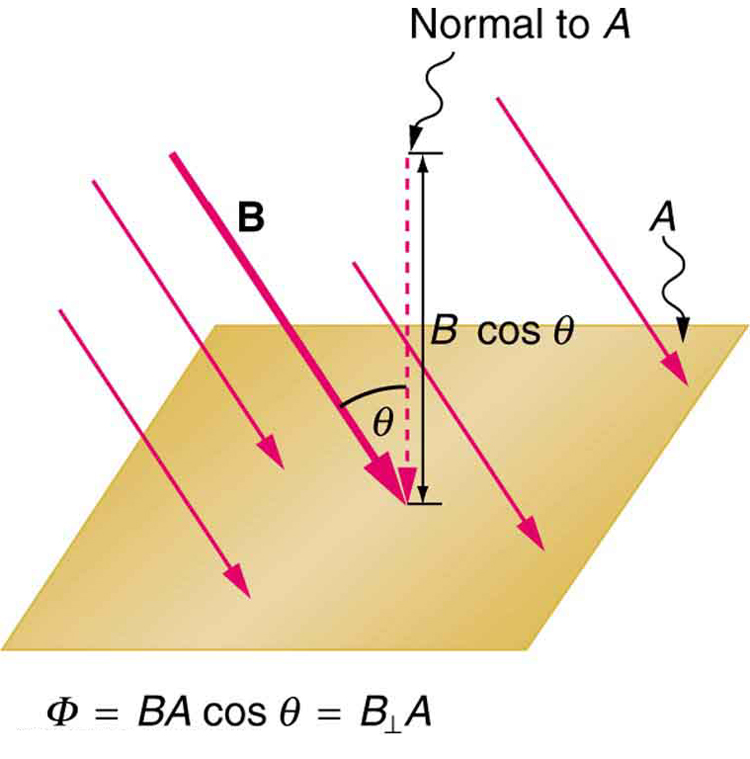
All induction, including the examples given so far, arises from some change in magnetic flux $latex \boldsymbol{\phi} $. For example, Faraday changed $latex \boldsymbol{B} $ and hence $latex \boldsymbol{\phi} $ when opening and closing the switch in his apparatus (shown in Figure 1). This is also true for the bar magnet and coil shown in Figure 2. When rotating the coil of a generator, the angle $latex \boldsymbol{\theta} $ and, hence, $latex \boldsymbol{\phi} $ is changed. Just how great an emf and what direction it takes depend on the change in $latex \boldsymbol{\phi} $ and how rapidly the change is made, as examined in the next section.

Conceptual Questions

1: How do the multiple-loop coils and iron ring in the version of Faraday’s apparatus shown in Figure 1 enhance the observation of induced emf?

2: When a magnet is thrust into a coil as in Figure 2(a), what is the direction of the force exerted by the coil on the magnet? Draw a diagram showing the direction of the current induced in the coil and the magnetic field it produces, to justify your response. How does the magnitude of the force depend on the resistance of the galvanometer?

3: Explain how magnetic flux can be zero when the magnetic field is not zero.

4: Is an emf induced in the coil in Figure 5 when it is stretched? If so, state why and give the direction of the induced current.

Problems & Exercises

1: What is the value of the magnetic flux at coil 2 in Figure 6 due to coil 1?

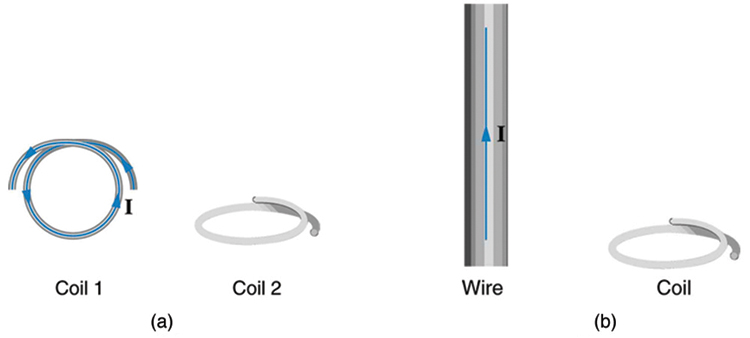
2: What is the value of the magnetic flux through the coil in Figure 6(b) due to the wire?