Formative Assessment

Rising, falling, swinging, bouncing, twirling, shaking. There are lots of ways that we describe motion in our everyday lives. We move to find food, to play, to socialize, to make art, to get new places, and so on. Even if we are sitting still, the tissues and organs in our body are constantly moving. We have lots of words to describe motion because motion is central to life.

Of course, precise descriptions and measurements of motion helps us to communicate with each other, but they also carry two additional benefits:

1. Predicting where something will be in the future
2. Knowing whether we understand what we observe happening

Benefit #1 – predicting future motion

If a child is moving by swinging, you can be confident that if you step away and come back in a minute, they will still be in the same general location. If a child is moving by running, they may get pretty far away if left alone for a minute. On the other hand, a child moving by walking won’t go so far. The better we know how something is moving, the better we can guess where it will be in the future. Similarly, the better – or more precisely – we can describe motion, the more precisely we can where it will be in the future.

Benefit #2 – knowing whether we understand what we see

Suppose a friend told you that they dropped a rock and it fell to the ground. You’d likely not thing anything of it (except perhaps that you need to find friends who tell better stories). But supposed that friend told you they dropped a rock and it started bouncing. You would know that there is something funny about either the rock or the ground. Sometimes the unexpected motion can be more subtle than bouncing versus dropping – physicians use a special type of ultrasound (called doppler ultrasound) to measure how quickly blood moves in the heart as it pumps. Relatively small variations from normal blood flow speeds can be an indication of an underlying problem, prompting further investigation of heart function.

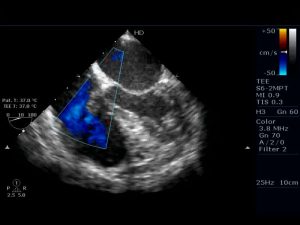
Precise descriptions of motion can let us know whether we understand what is going on in the world around us or whether there is something more to know.

How can we precisely describe motion?

In most everyday situations, using words like shaking, twisting, or falling are usually plenty adequate to describe how things move. But we often need more detail. If someone asks for directions to Cedar Rapids, it’s not too helpful to simply say, “Go north.” Likewise, if a friend is traveling from Cedar Rapids to meet you, it would be good to know whether they are coming with a car or a bicycle. When describing motion, we need clear ways to communicate where things are and how fast they move. This is the idea of position and speed.

Position

On the Earth’s surface, we communicate where cities are by a system of latitude and longitude. Iowa City is located at 41.66°N and 91.53°W. North of what? The equator. West of what? Greenwich, England (why Greenwich? Good question…suffice it to say, it took people a long time to agree about this). What’s at 0°N and 0°W? This attractive-looking buoy:

So every time you see a latitude and longitude, it tells you its location on Earth’s surface relative to the buoy that scientists have permanently moored at 0°N and 0°W.

In general, describing where something is must be done relative to something else. Cedar Rapids is about 30 miles north of Iowa City. The peak of Mount Everest is about 29,000 feet above sea level. To fully describe our position, we need TWO pieces of information:

1. Distance from a reference point
2. Direction that we must travel from the reference point to get to where we are

Describing distance

To describe a distance, we can of course say “near” or “far”, but to be more precise, we need a unit of measure. This could be miles, feet, or even Smoots. People also describe distances in fathoms, parsecs, hands, nautical miles, and so on. Many years ago communicating about distances was a mess – different people used different units, and as people from different places began chatting more often about how far things are, they decided upon a standard international system. They agreed that the standard measure of length would be the meter, which they originally defined as 1/10,000,000 the distance between the North Pole and the equator (along a line passing through Paris! Scandalous).

Of course, not everyone has agreed to use the meter. Here in the US, we stuck with feet, inches, and miles – known as the imperial system. Originally, measures in the imperial system were defined using the human body, which makes little sense since – you know – people are different sizes. More recently, they figured out a way to precisely define units like the foot – it is exactly 0.3048 meters. Yes, imperial units are officially defined in terms of their metric equivalents.

The metric system has the great advantage that it is easier to switch between units. A kilometer is 1000 meters. There are 100 centimeters in a meter. A person 1.83 meters tall is 183 centimeters tall. In the US, the imperial system has the great advantage that we grow up using these units and develop an intuition for them. It is more difficult to switch between units in the imperial system. How many inches tall is a person who is 3’8″? Take 3 times 12 inches, then add 8. (Ugh…) Using imperial units is more intuitive in our everyday (American) lives, but gets quickly annoying if you start needing to, say, add 13’7″ to 6’9″. For this reason, scientists usually stick to metric units to make calculations and communication easier (but it takes time to develop an intuitive feel for units you’re not used to!).

Describing direction

Direction tells you which way you’re pointed. That’s it. To describe direction, people commonly use the compass directions, in which North points toward the Earth’s North Pole. Beginning with north, east, south, and west, we can add in-between directions, such as northeast, halfway between north and east. From there we can further specify just north of northeast, or north-northeast.

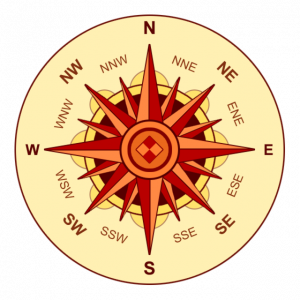
To be more precise, it makes sense to describe direction in terms of an angle away from North. You must turn 90° from north to face east, for example. The compass below gives directions in terms of degrees.

An angle tells you how far you have to turn from a reference direction (say, north) to point in the correct direction. Like distance, there is more than one way to measure an angle. People commonly use degrees and radians. To turn in a full circle, you must turn 360°. Radians are useful for lots of things, but everyday life is not one of them. We’ll ignore them. Adding “up” and “down” to the arrows on a compass needle is enough to describe any possible direction.

To describe your position precisely, you must clearly communicate your distance away from some reference point and the direction to travel away from it.

Speed

When we move, we change our position. And of course we can do this quickly or slowly. One way to describe how quickly we move is to do so in terms of how long it takes us to move a set distance. For example, Eliud Kipchoge set a world record in the marathon by running 26.2 miles in just over 2 hours (2:01:36). To do this, he ran each mile in under 0.08 hour.

Though it probably makes more intuitive sense to say that his speed was about 12.9 miles per hour. Those runners out there might have a better intuition for saying that he ran with a pace of 4:39 minutes per mile. 

When we describe speed, we typically talk in terms of how far we would move if we kept up the same speed for a certain period of time. For example, our speed in miles per hour tells us how far we would go if we traveled at that speed for an hour. Miles per hour works well for everyday speeds. Some things move very slowly, like glaciers, and a unit like inches per year or centimeters per year make more sense.

In general, to calculate a numerical value for speed, we divide the distance something moved by the time it took to move that far, or:

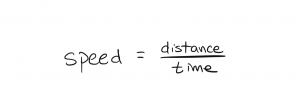
The units assigned to speed is therefore always a distance unit divided by a time unit. In the US, we commonly conceptualize speed as miles/hour (mi/h or mph), but in metric countries and scientific settings, units like meters/second (m/s) and kilometers per hour (km/h) are more common.

Speed tells you how far something moves in a certain time. You might have also heard the term “velocity”. The difference is that velocity includes your direction of motion. Technically, velocity is calculated as:

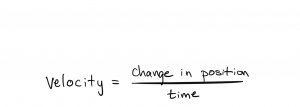
Remember that position describes a location in terms of distance AND direction from a reference point (e.g., 50 miles north of Iowa City). Thus, because velocity describes how quickly position changes, it includes information about both the speed AND direction of motion. Roads have “speed” limits because they care about how much distance you cover per time. You are allowed to travel in either direction on the road, so there are not velocity limits.

Who cares about the difference between speed and velocity? Very few people in an everyday setting. But when we begin to think about why motion is exciting for kids, it turns out that velocity – or at least changing velocity – is a very important idea.

Changes in motion

Moving the same way all the time is boring. If you’ve ever been traveling 200 mph on a high-speed train or 500 mph in an airplane, you mostly feel like you’re just sitting there. But roller coasters twist and turn and go faster and slower at different points in the ride. They change speed AND direction to make it fun, that is, they change their velocity to be exciting.

Changes in speed and direction are exciting, but there is a limit between exciting and dangerous. In August 2021, a roller coaster called Do-Dodonpa in Japan had to close down because of spate of broken bones among passengers. The Do-Dodonpa is not the world’s fastest (highest speed) roller coaster, but it is the worlds fastest-accelerating roller coaster. Speed itself isn’t so dangerous. Acceleration can be.

Velocity describes how fast your position changes, and acceleration describes how fast your velocity changes. You’ve probably heard people bragging about how fast their sports car goes from “zero to sixty”. This is their acceleration. Some of the fastest production cars today go from 0-60 mph in 2 seconds. So, their speed increases by 30mph every second. You could say, then, that their acceleration is 30 mph per second. To calculate acceleration, you can do it like this:

The units on acceleration end up being a little funny since it is the rate at which speed changes. Since speed is also a rate (distance per time), then acceleration is the rate at which another rate changes. So acceleration can be:

• miles PER hour PER second (that is, how many miles per hour your speed changes per second). We can write this as mph/s.
• meters PER second PER second (that is, how many meters per second your speed changes per second). We can write this as m/s/s, or even m/s².

Acceleration, like velocity, has both a magnitude (size) and a direction. That is, you can speed up in a particular direction – you speed up toward the ground as you fall. When a rocket is launched, it speeds up toward the sky. Interestingly, you can also accelerate while staying at the SAME SPEED. How? By changing direction. A twisty slide is fun because it is exciting to feel acceleration. A merry-go-round spinning at a constant speed feels different than sitting on a train going a constant speed because on the merry-go-round, the direction of our motion is changing as we go around a circle – we accelerate because we are changing direction. Speeding up, slowing down, or changing direction – these are all ways that we can accelerate, and all can make for exciting experiences on a playground. But accelerations that are too big can be dangerous. In the next chapter, we will begin to discuss why this is so – it all has to do with force.

Performance Expectations

Disciplinary Core Ideas

PS2.A: Forces and Motion

• Pushes and pulls can have different strengths and directions.
• Pushing or pulling on an object can change the speed or direction of its motion and can start or stop it.

Crosscutting Concepts

Patterns

• Patterns of change can be used to make predictions. (3-PS2-2)